Decagon

Multi tool use
| Regular decagon | |
|---|---|
 A regular decagon | |
| Type | Regular polygon |
Edges and vertices | 10 |
| Schläfli symbol | 10, t5 |
| Coxeter diagram | |
| Symmetry group | Dihedral (D10), order 2×10 |
Internal angle (degrees) | 144° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a decagon is a ten-sided polygon or 10-gon.[1]
Contents
1 Regular decagon
1.1 Area
1.2 Sides
1.3 Construction
1.4 Nonconvex regular decagon
2 The golden ratio in decagon
3 Symmetry
4 Dissection
5 Skew decagon
5.1 Petrie polygons
6 See also
7 References
8 External links
Regular decagon
A regular decagon has all sides of equal length and each internal angle will always be equal to 144°.[1] Its Schläfli symbol is 10 [2] and can also be constructed as a truncated pentagon, t5, a quasiregular decagon alternating two types of edges.
Area
The area of a regular decagon of side length a is given by:[3]
- A=52a2cot(π10)=52a25+25≃7.694208843a2displaystyle A=frac 52a^2cot left(frac pi 10right)=frac 52a^2sqrt 5+2sqrt 5simeq 7.694208843,a^2
In terms of the apothem r (see also inscribed figure), the area is:
- A=10tan(π10)r2=5r25−25≃3.249196963r2displaystyle A=10tan left(frac pi 10right)r^2=5r^2sqrt 5-2sqrt 5simeq 3.249196963,r^2
In terms of the circumradius R, the area is:
- A=52sin(π5)R2=52R25−52≃2.938926262R2displaystyle A=frac 52sin left(frac pi 5right)R^2=frac 52R^2sqrt frac 5-sqrt 52simeq 2.938926262,R^2
An alternative formula is A=2.5dadisplaystyle A=2.5da
By simple trigonometry,
- d=2a(cos3π10+cosπ10),displaystyle d=2aleft(cos tfrac 3pi 10+cos tfrac pi 10right),
and it can be written algebraically as
- d=a5+25.displaystyle d=asqrt 5+2sqrt 5.
Sides
The side of a regular decagon inscribed in a unit circle is −1+52=1ϕdisplaystyle tfrac -1+sqrt 52=tfrac 1phi 

Construction
As 10 = 2 × 5, a power of two times a Fermat prime, it follows that a regular decagon is constructible using compass and straightedge, or by an edge-bisection of a regular pentagon.[4]
@media all and (max-width:720px).mw-parser-output .tmulti>.thumbinnerwidth:100%!important;max-width:none!important.mw-parser-output .tmulti .tsinglefloat:none!important;max-width:none!important;width:100%!important;text-align:center


An alternative (but similar) method is as follows:
- Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
- Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon.
- The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.
Nonconvex regular decagon

This tiling by golden triangles, a regular pentagon, contains a stellation of regular decagon, the Schäfli symbol of which is 10/3.
The length ratio of two inequal edges of a golden triangle is the golden ratio, denoted by Φ,displaystyle textby Phi text,
- Φ−1=1Φ=2cos72∘=12cos36∘=5−12.displaystyle Phi -1=frac 1Phi =2,cos 72,^circ =frac 1,2,cos 36,^circ =frac ,sqrt 5-1,2text.
So we can get the properties of a regular decagonal star, through a tiling by golden triangles that fills this star polygon.
The golden ratio in decagon
Both in the construction with given circumcircle[5] as well as with given side length is the golden ratio dividing a line segment by exterior division the
determining construction element.
- In the construction with given circumcircle the circular arc around G with radius GE3 produces the segment AH, whose division corresponds to the golden ratio.
- AM¯MH¯=AH¯AM¯=1+52=Φ≈1.618.displaystyle frac overline AMoverline MH=frac overline AHoverline AM=frac 1+sqrt 52=Phi approx 1.618text.
- In the construction with given side length[6] the circular arc around D with radius DA produces the segment E10F, whose division corresponds to the golden ratio.
- E1E10¯E1F¯=E10F¯E1E10¯=Ra=1+52=Φ≈1.618.displaystyle frac overline E_1E_10overline E_1F=frac overline E_10Foverline E_1E_10=frac Ra=frac 1+sqrt 52=Phi approx 1.618text.


Symmetry

Symmetries of a regular decagon. Vertices are colored by their symmetry positions. Blue mirrors are drawn through vertices, and purple mirrors are drawn through edges. Gyration orders are given in the center.
The regular decagon has Dih10 symmetry, order 20. There are 3 subgroup dihedral symmetries: Dih5, Dih2, and Dih1, and 4 cyclic group symmetries: Z10, Z5, Z2, and Z1.
These 8 symmetries can be seen in 10 distinct symmetries on the decagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order.[7] Full symmetry of the regular form is r20 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g10 subgroup has no degrees of freedom but can seen as directed edges.
The highest symmetry irregular decagons are d10, a isogonal decagon constructed by five mirrors which can alternate long and short edges, and p10, an isotoxal decagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular decagon.
Dissection
10-cube projection | 40 rhomb dissection | |||
|---|---|---|---|---|
 |  |  |  |  |
 | 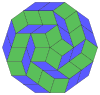 | 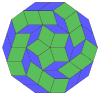 |  |  |
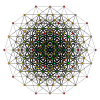
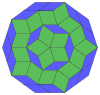
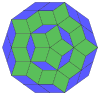
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.[8]
In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular decagon, m=5, and it can be divided into 10 rhombs, with examples shown below. This decomposition can be seen as 10 of 80 faces in a Petrie polygon projection plane of the 5-cube. A dissection is based on 10 of 30 faces of the rhombic triacontahedron. The list OEIS: A006245 defines the number of solutions as 62, with 2 orientations for the first symmetric form, and 10 orientations for the other 6.
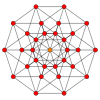 5-cube | 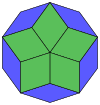 |  | 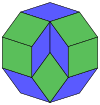 |
 |  |  | 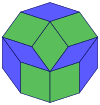 |
Skew decagon
| 5# | 5/2# | 5/3# |
|---|---|---|
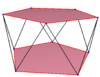 | 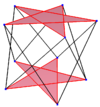 |  |
| A regular skew decagon is seen as zig-zagging edges of a pentagonal antiprism, a pentagrammic antiprism, and a pentagrammic crossed-antiprism. | ||
A skew decagon is a skew polygon with 10 vertices and edges but not existing on the same plane. The interior of such an decagon is not generally defined. A skew zig-zag decagon has vertices alternating between two parallel planes.
A regular skew decagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew decagon and can be seen in the vertices and side edges of a pentagonal antiprism, pentagrammic antiprism, and pentagrammic crossed-antiprism with the same D5d, [2+,10] symmetry, order 20.
These can also be seen in these 4 convex polyhedra with icosahedral symmetry. The polygons on the perimeter of these projections are regular skew decagons.
 Dodecahedron | 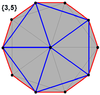 Icosahedron | 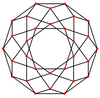 Icosidodecahedron | 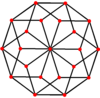 Rhombic triacontahedron |
Petrie polygons
The regular skew decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these orthogonal projections in various Coxeter planes:[9] The number of sides in the Petrie polygon is equal to the Coxeter number, h, for each symmetry family.
| A9 | D6 | B5 | ||
|---|---|---|---|---|
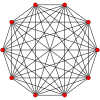 9-simplex | 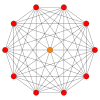 411 | 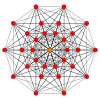 131 |  5-orthoplex |  5-cube |
See also
Decagonal number and centered decagonal number, figurate numbers modeled on the decagon
Decagram, a star polygon with the same vertex positions as the regular decagon
References
^ ab Sidebotham, Thomas H. (2003), The A to Z of Mathematics: A Basic Guide, John Wiley & Sons, p. 146, ISBN 9780471461630.mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em.
^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595.
^ The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59. Note that this source uses a as the edge length and gives the argument of the cotangent as an angle in degrees rather than in radians.
^ ab Ludlow, Henry H. (1904), Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle, The Open Court Publishing Co..
^ ab Green, Henry (1861), Euclid's Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II, London: Simpkin, Marshall,& CO., p. 116. Retrieved 10 February 2016.
^ ab (in German) Köller, Jürgen (2005), Regelmäßiges Zehneck, → 3. Section "Formeln, Ist die Seite a gegeben ...". Retrieved 10 February 2016.
^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things,
ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
^ Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.
External links
- Weisstein, Eric W. "Decagon". MathWorld.
Definition and properties of a decagon With interactive animation
GtZ0IUX







