Odtnhj

In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced (Coxeter 1934) as abstractions of reflection groups, and finite Coxeter groups were classified in 1935 (Coxeter 1935).

Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytopes, and the Weyl groups of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras.

Standard references include (Humphreys 1992) and (Davis 2007).

Definition

Formally, a Coxeter group can be defined as a group with the presentation

leftlangle r_1,r_2,ldots ,r_nmid (r_ir_j)^m_ij=1rightrangle

where $m_ii=1$ and $m_ijgeq 2$ for $ineq j$ .
The condition $displaystyle m_ij=infty$ means no relation of the form $displaystyle (r_ir_j)^m$ should be imposed.

The pair $(W,S)$ where $W$ is a Coxeter group with generators $displaystyle S=r_1,dots ,r_n$ is called a Coxeter system. Note that in general $S$ is not uniquely determined by $W$ . For example, the Coxeter groups of type $B_3$ and $displaystyle A_1times A_3$ are isomorphic but the Coxeter systems are not equivalent (see below for an explanation of this notation).

A number of conclusions can be drawn immediately from the above definition.

The relation $displaystyle m_ii=1$ means that $displaystyle (r_ir_i)^1=(r_i)^2=1$ for all $i$ ; as such the generators are involutions.

If $displaystyle m_ij=2$ , then the generators $r_i$ and $r_j$ commute. This follows by observing that

displaystyle xx=yy=1

,

together with

displaystyle xyxy=1

implies that

displaystyle xy=x(xyxy)y=(xx)yx(yy)=yx

.

Alternatively, since the generators are involutions,

r_i=r_i^-1

, so

(r_ir_j)^2=r_ir_jr_ir_j=r_ir_jr_i^-1r_j^-1

, and thus is equal to the commutator.

In order to avoid redundancy among the relations, it is necessary to assume that $m_ij=m_ji$ . This follows by observing that

displaystyle yy=1

,

together with

displaystyle (xy)^m=1

implies that

displaystyle (yx)^m=(yx)^myy=y(xy)^my=yy=1

.

Alternatively,

(xy)^k

and

(yx)^k

are conjugate elements, as

y(xy)^ky^-1=(yx)^kyy^-1=(yx)^k

.

Coxeter matrix and Schläfli matrix

The Coxeter matrix is the $ntimes n$ , symmetric matrix with entries $m_ij$ . Indeed, every symmetric matrix with diagonal entries exclusively 1 and nondiagonal entries in the set $displaystyle 2,3,ldots cup infty$ is a Coxeter matrix.

The Coxeter matrix can be conveniently encoded by a Coxeter diagram, as per the following rules.

The vertices of the graph are labelled by generator subscripts.

Vertices $i$ and $j$ are adjacent if and only if $displaystyle m_ijgeq 3$ .

An edge is labelled with the value of $m_ij$ whenever the value is $4$ or greater.

In particular, two generators commute if and only if they are not connected by an edge.
Furthermore, if a Coxeter graph has two or more connected components, the associated group is the direct product of the groups associated to the individual components.
Thus the disjoint union of Coxeter graphs yields a direct product of Coxeter groups.

The Coxeter matrix, $M_ij$ , is related to the $ntimes n$ Schläfli matrix $C$ with entries $displaystyle C_ij=-2cos(pi /M_ij)$ , but the elements are modified, being proportional to the dot product of the pairwise generators. The Schläfli matrix is useful because its eigenvalues determine whether the Coxeter group is of finite type (all positive), affine type (all non-negative, at least one zero), or indefinite type (otherwise). The indefinite type is sometimes further subdivided, e.g. into hyperbolic and other Coxeter groups. However, there are multiple non-equivalent definitions for hyperbolic Coxeter groups.

Examples
Coxeter group	A₁×A₁	A₂	B₂	H₂	G₂	$tilde I_1$	A₃	B₃	D₄	$tilde A_3$
Coxeter diagram
Coxeter matrix	$left[beginsmallmatrix1&2\2&1\endsmallmatrixright]$	$left[beginsmallmatrix1&3\3&1\endsmallmatrixright]$	$displaystyle left[beginsmallmatrix1&4\4&1\endsmallmatrixright]$	$displaystyle left[beginsmallmatrix1&5\5&1\endsmallmatrixright]$	$displaystyle left[beginsmallmatrix1&6\6&1\endsmallmatrixright]$	$left[beginsmallmatrix1&infty \infty &1\endsmallmatrixright]$	$left[beginsmallmatrix1&3&2\3&1&3\2&3&1endsmallmatrixright]$	$left[beginsmallmatrix1&4&2\4&1&3\2&3&1endsmallmatrixright]$	$left[beginsmallmatrix1&3&2&2\3&1&3&3\2&3&1&2\2&3&2&1endsmallmatrixright]$	$left[beginsmallmatrix1&3&2&3\3&1&3&2\2&3&1&3\3&2&3&1endsmallmatrixright]$
Schläfli matrix	$left[beginsmallmatrix2&0\0&2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-1\-1& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-sqrt 2\-sqrt 2& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-phi \-phi & ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-sqrt 3\-sqrt 3& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-2\-2& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-1& ,0\-1& ,2&-1\ ,0&-1& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix , 2&-sqrt 2& ,0\-sqrt 2& , 2&-1\ , 0& ,-1& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-1& ,0& ,0\-1& ,2&-1&-1\ ,0&-1& ,2& ,0\ ,0&-1& ,0& ,2endsmallmatrixright]$	$displaystyle left[beginsmallmatrix ,2&-1& ,0&-1\-1& ,2&-1& ,0\ ,0&-1& ,2&-1\-1& ,0&-1& ,2endsmallmatrixright]$

An example

The graph $A_n$ in which vertices 1 through n are placed in a row with each vertex connected by an unlabelled edge to its immediate neighbors gives rise to the symmetric group S_n+1; the generators correspond to the transpositions (1 2), (2 3), ... , (n n+1). Two non-consecutive transpositions always commute, while (k k+1) (k+1 k+2) gives the 3-cycle (k k+2 k+1). Of course, this only shows that S_n+1 is a quotient group of the Coxeter group described by the graph, but it is not too difficult to check that equality holds.

Connection with reflection groups

Coxeter groups are deeply connected with reflection groups. Simply put, Coxeter groups are abstract groups (given via a presentation), while reflection groups are concrete groups (given as subgroups of linear groups or various generalizations). Coxeter groups grew out of the study of reflection groups — they are an abstraction: a reflection group is a subgroup of a linear group generated by reflections (which have order 2), while a Coxeter group is an abstract group generated by involutions (elements of order 2, abstracting from reflections), and whose relations have a certain form ( $(r_ir_j)^k$ , corresponding to hyperplanes meeting at an angle of $pi /k$ , with $r_ir_j$ being of order k abstracting from a rotation by $2pi /k$ ).

The abstract group of a reflection group is a Coxeter group, while conversely a reflection group can be seen as a linear representation of a Coxeter group. For finite reflection groups, this yields an exact correspondence: every finite Coxeter group admits a faithful representation as a finite reflection group of some Euclidean space. For infinite Coxeter groups, however, a Coxeter group may not admit a representation as a reflection group.

Historically, (Coxeter 1934) proved that every reflection group is a Coxeter group (i.e., has a presentation where all relations are of the form $r_i^2$ or $(r_ir_j)^k$ ), and indeed this paper introduced the notion of a Coxeter group, while (Coxeter 1935) proved that every finite Coxeter group had a representation as a reflection group, and classified finite Coxeter groups.

Finite Coxeter groups

Coxeter graphs of the finite Coxeter groups.

Classification

The finite Coxeter groups were classified in (Coxeter 1935), in terms of Coxeter–Dynkin diagrams; they are all represented by reflection groups of finite-dimensional Euclidean spaces.

The finite Coxeter groups consist of three one-parameter families of increasing rank $A_n,B_n,D_n,$ one one-parameter family of dimension two, $I_2(p),$ and six exceptional groups: $E_6,E_7,E_8,F_4,H_3,$ and $H_4.$

Weyl groups

Many, but not all of these, are Weyl groups, and every Weyl group can be realized as a Coxeter group. The Weyl groups are the families $A_n,B_n,$ and $D_n,$ and the exceptions $E_6,E_7,E_8,F_4,$ and $I_2(6),$ denoted in Weyl group notation as $G_2.$ The non-Weyl groups are the exceptions $H_3$ and $H_4,$ and the family $I_2(p)$ except where this coincides with one of the Weyl groups (namely $I_2(3)cong A_2,I_2(4)cong B_2,$ and $I_2(6)cong G_2$ ).

This can be proven by comparing the restrictions on (undirected) Dynkin diagrams with the restrictions on Coxeter diagrams of finite groups: formally, the Coxeter graph can be obtained from the Dynkin diagram by discarding the direction of the edges, and replacing every double edge with an edge labelled 4 and every triple edge by an edge labelled 6. Also note that every finitely generated Coxeter group is an automatic group.^[1] Dynkin diagrams have the additional restriction that the only permitted edge labels are 2, 3, 4, and 6, which yields the above. Geometrically, this corresponds to the crystallographic restriction theorem, and the fact that excluded polytopes do not fill space or tile the plane – for $H_3,$ the dodecahedron (dually, icosahedron) does not fill space; for $H_4,$ the 120-cell (dually, 600-cell) does not fill space; for $I_2(p)$ a p-gon does not tile the plane except for $p=3,4,$ or $6$ (the triangular, square, and hexagonal tilings, respectively).

Note further that the (directed) Dynkin diagrams B_n and C_n give rise to the same Weyl group (hence Coxeter group), because they differ as directed graphs, but agree as undirected graphs – direction matters for root systems but not for the Weyl group; this corresponds to the hypercube and cross-polytope being different regular polytopes but having the same symmetry group.

Properties

Some properties of the finite irreducible Coxeter groups are given in the following table. The order of reducible groups can be computed by the product of their irreducible subgroup orders.

Rank n	Group symbol	Alternate symbol	Bracket notation	Coxeter graph	Reflections m = nh/2^[2]	Coxeter number h	Order	Related polytopes
1	A₁	A₁	[ ]		1	2	2
2	A₂	A₂	[3]		3	3	6	3
3	A₃	A₃	[3,3]		6	4	24	3,3
4	A₄	A₄	[3,3,3]		10	5	120	3,3,3
5	A₅	A₅	[3,3,3,3]		15	6	720	3,3,3,3
6	A₆	A₆	[3,3,3,3,3]		21	7	5040	3,3,3,3,3
7	A₇	A₇	[3,3,3,3,3,3]		28	8	40320	3,3,3,3,3,3
8	A₈	A₈	[3,3,3,3,3,3,3]		36	9	362880	3,3,3,3,3,3,3
n	A_n	A_n	[3ⁿ⁻¹]	...	n(n + 1)/2	n + 1	(n + 1)!	n-simplex
2	B₂	C₂	[4]		4	4	8	4
3	B₃	C₃	[4,3]		9	6	48	4,3 / 3,4
4	B₄	C₄	[4,3,3]		16	8	384	-4,3,3 / 3,3,4
5	B₅	C₅	[4,3,3,3]		25	10	3840	4,3,3,3 / 3,3,3,4
6	B₆	C₆	[4,3,3,3,3]		36	12	46080	4,3,3,3,3 / 3,3,3,3,4
7	B₇	C₇	[4,3,3,3,3,3]		49	14	645120	4,3,3,3,3,3 / 3,3,3,3,3,4
8	B₈	C₈	[4,3,3,3,3,3,3]		64	16	10321920	4,3,3,3,3,3 / 3,3,3,3,3,4
n	B_n	C_n	[4,3ⁿ⁻²]	...	n²	2n	2ⁿn!	n-cube / n-orthoplex
4	D₄	B₄	[3^1,1,1]		12	6	192	h4,3,3 / 3,3^1,1
5	D₅	B₅	[3^2,1,1]		20	8	1920	h4,3,3,3 / 3,3,3^1,1
6	D₆	B₆	[3^3,1,1]		30	10	23040	h4,3,3,3,3 / 3,3,3,3^1,1
7	D₇	B₇	[3^4,1,1]		42	12	322560	h4,3,3,3,3,3 / 3,3,3,3,3^1,1
8	D₈	B₈	[3^5,1,1]		56	14	5160960	h4,3,3,3,3,3,3 / 3,3,3,3,3,3^1,1
n	D_n	B_n	[3^n−3,1,1]	...	n(n − 1)	2(n − 1)	2ⁿ⁻¹n!	n-demicube / n-orthoplex
6	E₆	E₆	[3^2,2,1]		36	12	51840 (72x6!)	2₂₁, 1₂₂
7	E₇	E₇	[3^3,2,1]		63	18	2903040 (72x8!)	3₂₁, 2₃₁, 1₃₂
8	E₈	E₈	[3^4,2,1]		120	30	696729600 (192x10!)	4₂₁, 2₄₁, 1₄₂
4	F₄	F₄	[3,4,3]		24	12	1152	3,4,3
2	G₂	–	[6]		6	6	12	6
2	H₂	G₂	[5]		5	5	10	5
3	H₃	G₃	[3,5]		15	10	120	3,5 / 5,3
4	H₄	G₄	[3,3,5]		60	30	14400	5,3,3 / 3,3,5
2	I₂(p)	D^p ₂	[p]		p	p	2p	p

Symmetry groups of regular polytopes

All symmetry groups of regular polytopes are finite Coxeter groups. Note that dual polytopes have the same symmetry group.

There are three series of regular polytopes in all dimensions. The symmetry group of a regular n-simplex is the symmetric group S_n+1, also known as the Coxeter group of type A_n. The symmetry group of the n-cube and its dual, the n-cross-polytope, is B_n, and is known as the hyperoctahedral group.

The exceptional regular polytopes in dimensions two, three, and four, correspond to other Coxeter groups. In two dimensions, the dihedral groups, which are the symmetry groups of regular polygons, form the series I₂(p). In three dimensions, the symmetry group of the regular dodecahedron and its dual, the regular icosahedron, is H₃, known as the full icosahedral group. In four dimensions, there are three special regular polytopes, the 24-cell, the 120-cell, and the 600-cell. The first has symmetry group F₄, while the other two are dual and have symmetry group H₄.

The Coxeter groups of type D_n, E₆, E₇, and E₈ are the symmetry groups of certain semiregular polytopes.

Table of irreducible polytope families

Family
n

n-simplex

n-hypercube

n-orthoplex

n-demicube

1_k2

2_k1

k₂₁

pentagonal polytope

Group

A_n

B_n

I₂(p)

D_n

E₆

E₇

E₈

F₄

G₂

H_n

2

Triangle

Square

p-gon
(example: p=7)

Hexagon

Pentagon

3

Tetrahedron

Cube

Octahedron

Tetrahedron

Dodecahedron

Icosahedron

4

5-cell

Tesseract

16-cell

Demitesseract

24-cell

120-cell

600-cell

5

5-simplex

5-cube

5-orthoplex

5-demicube

6

6-simplex

6-cube

6-orthoplex

6-demicube

1₂₂

2₂₁

7

7-simplex

7-cube

7-orthoplex

7-demicube

1₃₂

2₃₁

3₂₁

8

8-simplex

8-cube

8-orthoplex

8-demicube

1₄₂

2₄₁

4₂₁

9

9-simplex

9-cube

9-orthoplex

9-demicube

10

10-simplex

10-cube

10-orthoplex

10-demicube

Affine Coxeter groups

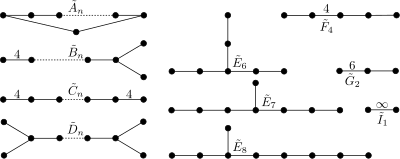
Coxeter diagrams for the Affine Coxeter groups

Stiefel diagram for the

G_2

root system

The affine Coxeter groups form a second important series of Coxeter groups. These are not finite themselves, but each contains a normal abelian subgroup such that the corresponding quotient group is finite. In each case, the quotient group is itself a Coxeter group, and the Coxeter graph of the affine Coxeter group is obtained from the Coxeter graph of the quotient group by adding another vertex and one or two additional edges. For example, for n ≥ 2, the graph consisting of n+1 vertices in a circle is obtained from A_n in this way, and the corresponding Coxeter group is the affine Weyl group of A_n. For n = 2, this can be pictured as a subgroup of the symmetry group of the standard tiling of the plane by equilateral triangles.

In general, given a root system, one can construct the associated Stiefel diagram, consisting of the hyperplanes orthogonal to the roots along with certain translates of these hyperplanes. The affine Coxeter group (or affine Weyl group) is then the group generated by the (affine) reflections about all the hyperplanes in the diagram.^[3] The Stiefel diagram divides the plane into infinitely many connected components called alcoves, and the affine Coxeter group acts freely and transitively on the alcoves, just as the ordinary Weyl group acts freely and transitively on the Weyl chambers. The figure at right illustrates the Stiefel diagram for the $G_2$ root system.

Suppose $R$ is an irreducible root system of rank $r>1$ and let $displaystyle alpha _1,ldots ,alpha _r$ be a collection of simple roots. Let, also, $displaystyle alpha _r+1$ denote the highest root. Then the affine Coxeter group is generated by the ordinary (linear) reflections about the hyperplanes perpendicular to $displaystyle alpha _1,ldots ,alpha _r$ , together with an affine reflection about a translate of the hyperplane perpendicular to $displaystyle alpha _r+1$ . The Coxeter graph for the affine Weyl group is the Coxeter–Dynkin diagram for $R$ , together with one additional node associated to $displaystyle alpha _r+1$ . In this case, one alcove of the Stiefel diagram may be obtained by taking the fundamental Weyl chamber and cutting it by a translate of the hyperplane perpendicular to $displaystyle alpha _r+1$ .^[4]

A list of the affine Coxeter groups follows:

Group symbol	Witt symbol	Bracket notation	Coxeter graph	Related uniform tessellation(s)
$tilde A_n$	$P_n+1$	[3^[n]]	... or ...	Simplectic honeycomb
$tilde B_n$	$S_n+1$	[4,3ⁿ⁻³,3^1,1]	...	Demihypercubic honeycomb
$tilde C_n$	$R_n+1$	[4,3ⁿ⁻²,4]	...	Hypercubic honeycomb
$tilde D_n$	$displaystyle Q_n+1$	[ 3^1,1,3ⁿ⁻⁴,3^1,1]	...	Demihypercubic honeycomb
$tilde E_6$	$displaystyle T_7$	[3^2,2,2]	or	2₂₂
$tilde E_7$	$displaystyle T_8$	[3^3,3,1]	or	3₃₁, 1₃₃
$tilde E_8$	$displaystyle T_9$	[3^5,2,1]		5₂₁, 2₅₁, 1₅₂
$tilde F_4$	$displaystyle U_5$	[3,4,3,3]		16-cell honeycomb 24-cell honeycomb
$tilde G_2$	$displaystyle V_3$	[6,3]		Hexagonal tiling and Triangular tiling
$tilde I_1$	$displaystyle W_2$	[∞]		apeirogon

The group symbol subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's graph.

Hyperbolic Coxeter groups

There are infinitely many hyperbolic Coxeter groups describing reflection groups in hyperbolic space, notably including the hyperbolic triangle groups.

Partial orders

A choice of reflection generators gives rise to a length function l on a Coxeter group, namely the minimum number of uses of generators required to express a group element; this is precisely the length in the word metric in the Cayley graph. An expression for v using l(v) generators is a reduced word. For example, the permutation (13) in S₃ has two reduced words, (12)(23)(12) and (23)(12)(23). The function $vto (-1)^l(v)$ defines a map $Gto pm 1,$ generalizing the sign map for the symmetric group.

Using reduced words one may define three partial orders on the Coxeter group, the (right) weak order, the absolute order and the Bruhat order (named for François Bruhat). An element v exceeds an element u in the Bruhat order if some (or equivalently, any) reduced word for v contains a reduced word for u as a substring, where some letters (in any position) are dropped. In the weak order, v ≥ u if some reduced word for v contains a reduced word for u as an initial segment. Indeed, the word length makes this into a graded poset. The Hasse diagrams corresponding to these orders are objects of study, and are related to the Cayley graph determined by the generators. The absolute order is defined analogously to the weak order, but with generating set/alphabet consisting of all conjugates of the Coxeter generators.

For example, the permutation (1 2 3) in S₃ has only one reduced word, (12)(23), so covers (12) and (23) in the Bruhat order but only covers (12) in the weak order.

Homology

Since a Coxeter group $W$ is generated by finitely many elements of order 2, its abelianization is an elementary abelian 2-group, i.e., it is isomorphic to the direct sum of several copies of the cyclic group $Z_2$ . This may be restated in terms of the first homology group of $W$ .

The Schur multiplier $displaystyle M(W)$ , equal to the second homology group of $W$ , was computed in (Ihara & Yokonuma 1965) for finite reflection groups and in (Yokonuma 1965) for affine reflection groups, with a more unified account given in (Howlett 1988). In all cases, the Schur multiplier is also an elementary abelian 2-group. For each infinite family $displaystyle W_n$ of finite or affine Weyl groups, the rank of $displaystyle M(W_n)$ stabilizes as $n$ goes to infinity.

References

^ Brink, Brigitte; Howlett, RobertB. (1993), "A finiteness property and an automatic structure for Coxeter groups", Mathematische Annalen, 296 (1): 179–190, doi:10.1007/BF01445101, Zbl 0793.20036..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

^ Coxeter, Regular polytopes, §12.6 The number of reflections, equation 12.61

^ Hall 2015 Section 13.6

^ Hall 2015 Chapter 13, Exercises 12 and 13

External links

Hazewinkel, Michiel, ed. (2001) [1994], "Coxeter group", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4

Weisstein, Eric W. "Coxeter group". MathWorld.

Jenn software for visualizing the Cayley graphs of finite Coxeter groups on up to four generators

[BrinkAndHowlett-1] Brink, Brigitte; Howlett, RobertB. (1993), "A finiteness property and an automatic structure for Coxeter groups", Mathematische Annalen, 296 (1): 179–190, doi:10.1007/BF01445101, Zbl 0793.20036..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

[2] Coxeter, Regular polytopes, §12.6 The number of reflections, equation 12.61

[3] Hall 2015 Section 13.6

[4] Hall 2015 Chapter 13, Exercises 12 and 13

搜尋此網誌

Odtnhj

Coxeter group

Contents