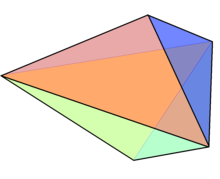
Triangular bipyramid
| Triangular bipyramid | |
|---|---|
 | |
| Type | Bipyramid and Johnson J11 - J12 - J13 |
| Faces | 6 triangles |
| Edges | 9 |
| Vertices | 5 |
| Schläfli symbol | + 3 |
| Coxeter diagram |     |
| Symmetry group | D3h, [3,2], (*223) order 12 |
| Rotation group | D3, [3,2]+, (223), order 6 |
| Dual polyhedron | Triangular prism |
| Face configuration | V3.4.4 |
| Properties | Convex, face-transitive |
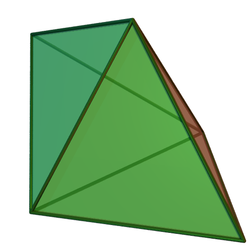
Net
In geometry, the triangular bipyramid (or dipyramid) is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.
As the name suggests, it can be constructed by joining two tetrahedra along one face. Although all its faces are congruent and the solid is face-transitive, it is not a Platonic solid because some vertices adjoin three faces and others adjoin four.
The bipyramid whose six faces are all equilateral triangles is one of the Johnson solids, (J12). A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1] As a Johnson solid with all faces equilateral triangles, it is also a deltahedron.
Contents
1 Dual polyhedron
2 Related polyhedra and honeycombs
3 See also
4 References
5 External links
Dual polyhedron
The dual polyhedron of the triangular bipyramid is the triangular prism, with five faces: two parallel equilateral triangles linked by a chain of three rectangles.
Although the triangular prism has a form that is a uniform polyhedron (with square faces), the dual of the Johnson solid form of the bipyramid has rectangular rather than square faces, and is not uniform.
| Dual triangular bipyramid | Net of dual |
|---|---|
 |  |
Related polyhedra and honeycombs
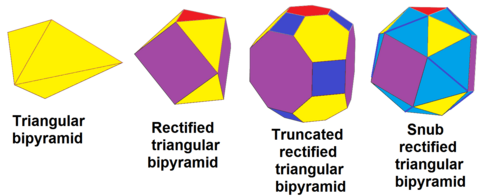
The triangular bipyramid, dt2,3, can be in sequence rectified, rdt2,3, truncated, trdt2,3 and alternated (snubbed), srdt2,3:
The triangular bipyramid can be constructed by augmentation of smaller ones, specifically two stacked regular octahedra with 3 triangular bipyramids added around the sides, and 1 tetrahedron above and below. This polyhedron has 24 equilateral triangle faces, but it is not a Johnson solid because it has coplanar faces. It is a coplanar 24-triangle deltahedron. This polyhedron exists as the augmentation of cells in a gyrated alternated cubic honeycomb. Larger triangular polyhedra can be generated similarly, like 9, 16 or 25 triangles per larger triangle face, seen as a section of a triangular tiling.
The triangular bipyramid can form a tessellation of space with octahedra or with truncated tetrahedra.[2]
 Layers of the uniform quarter cubic honeycomb can be shifted to pair up regular tetrahedral cells which combined into triangular bipyramids. | 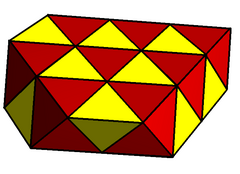 The gyrated tetrahedral-octahedral honeycomb has pairs of adjacent regular tetrahedra that can be seen as triangular bipyramids. |
When projected onto a sphere, it resembles a compound of a trigonal hosohedron and trigonal dihedron. It is part of an infinite series of dual pair compounds of regular polyhedra projected onto spheres. The triangular bipyramid can be referred to as a deltoidal hexahedron for consistency with the other solids in the series, although the "deltoids" are triangles instead of kites in this case, as the angle from the dihedron is 180 degrees.
| Symmetry *n32 [n,3] | Spherical | Euclid. | Compact hyperb. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Figure Config. |  V3.4.2.4 |  V3.4.3.4 |  V3.4.4.4 |  V3.4.5.4 |  V3.4.6.4 |  V3.4.7.4 |  V3.4.8.4 |  V3.4.∞.4 |
See also
- Trigonal bipyramidal molecular geometry
| Polyhedron |  |  |  |  |  |  |  |  | |
|---|---|---|---|---|---|---|---|---|---|
Coxeter | | |  |  |  |  |  |  |  |
| Tiling |  | |  |  |  |  |  |  |  |
Config. | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
References
^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em.
^ http://woodenpolyhedra.web.fc2.com/J12.html
External links
- Eric W. Weisstein, Triangular dipyramid (Johnson solid) at MathWorld.
Conway Notation for Polyhedra Try: dP3
