Odtnhj

Figure 1. Walter Kaufmann's measurement of the electron charge-to-mass ratio for different velocities of the electron. A radium source at the bottom of the evacuated apparatus emitted beta particles of varying energies. Parallel E and B fields in combination with the pinhole aperture allowed only certain combinations of electron direction and speed to expose the photographic plate at the top. (a) This front view of the apparatus illustrates the uniform acceleration imposed by the charged condenser plates on the beta particles. (b) This side view of the apparatus illustrates the circular motion of the beta particles transverse to the B field. (c) The photographic plate recorded a curved streak which was analyzed to determine e/m for varying v following different theoretical assumptions.

The Kaufmann–Bucherer–Neumann experiments measured the dependence of the inertial mass (or momentum) of an object on its velocity. The historical importance of this series of experiments performed by various physicists between 1901 and 1915 is due to the results being used to test the predictions of special relativity. The developing precision and data analysis of these experiments and the resulting influence on theoretical physics during those years is still a topic of active historical discussion, since the early experimental results at first contradicted Einstein's then newly published theory, but later versions of this experiment confirmed it. For modern experiments of that kind, see Tests of relativistic energy and momentum, for general information see Tests of special relativity.

Historical context

In 1896, Henri Becquerel discovered radioactive decay in a variety of chemical elements. Subsequently, the beta radiation from these decays was discovered to be the emission of a negatively charged particle. Later these particles were identified with the electron, discovered in cathode ray experiments by J. J. Thomson in 1897.

This was connected with the theoretical prediction of the electromagnetic mass by J. J. Thomson in 1881, who showed that the electromagnetic energy contributes to the mass of a moving charged body.^[1] Thomson (1893) and George Frederick Charles Searle (1897) also calculated that this mass depends on velocity, and that it becomes infinitely great when the body moves at the speed of light with respect to the luminiferous aether.^[2] Also Hendrik Antoon Lorentz (1899, 1900) assumed such a velocity dependence as a consequence of his theory of electrons.^[3] At this time, the electromagnetic mass was separated into "transverse" and "longitudinal" mass, and was sometimes denoted as "apparent mass", while the invariant Newtonian mass was denoted as "real mass".^{[A 1][A 2]} On the other hand, it was the belief of the German theoretician Max Abraham that all mass would ultimately prove to be of electromagnetic origin, and that Newtonian mechanics would become subsumed into the laws of electrodynamics.^{[A 3]}

The concept of (transverse) electromagnetic mass mTdisplaystyle m_T, which was based on specific models of the electron, was later transmuted into the purely kinematical concept of relativistic mass which concerns all forms of energy, not only electromagnetic energy. Currently, however, the concept of relativistic mass, although still frequently referred to in popular works on relativity, is now seldom used among professional working physicists, and has been superseded by the expressions for relativistic energy and momentum, which also predict that the speed of light cannot be reached by massive bodies. This is because all of those relations involve the Lorentz factor:

mTm=pmv=Emc2=11−v2c2displaystyle frac m_Tm=frac pmv=frac Emc^2=frac 1sqrt 1-frac v^2c^2

Therefore, the Bucherer–Kaufmann–Neumann experiments can be seen as early tests of relativistic energy and momentum. (For the following historical description of the experiments, the concepts of "transverse" or "relativistic mass" are still used).

Kaufmann's experiments

First experiments

Figure 2. Kaufmann's measurements of 1901 (corrected in 1902) showed that the charge-to-mass ratio diminishes and thus the electron's momentum (or mass) increases with velocity. Note that ϵ/m0∼1.76×107displaystyle scriptstyle epsilon /m_0sim 1.76times 10^7 emu/gm when the electron is at rest.

Walter Kaufmann began to experiment with beta rays using a device similar to a cathode ray tube, where the source of the electrons was the decay of radium that was placed in an evacuated container. (See Fig. 1) Such rays emitted from radium were called "Becquerel rays" at that time. Contrary to the then known cathode rays which reached speeds only up to 0.3c, c being the speed of light, Becquerel rays reached velocities up to 0.9c. However, since beta particles have different velocities, the radiation was inhomogeneous. Therefore, Kaufmann applied electric and magnetic fields aligned parallel to each other, so that the deflections caused by them were perpendicular to each other. Their impacts on a photographic plate produced a deflection curve, whose individual points corresponded to a certain velocity and a certain mass of the electrons. By reversing the charge on the condenser, thus inverting the electric field, two symmetric curves could be obtained, whose center line determined the direction of the magnetic deflection.^{[A 4][A 5]}

Kaufmann published a first analysis of his data in 1901 – he actually was able to measure a decrease of the charge-to-mass ratio, thus demonstrating that mass or momentum increases with velocity.^[4] Using Searle's formula (1897) for the electromagnetic energy increase of charged bodies with velocity, he calculated the increase of the electron's electromagnetic mass as a function of velocity:

ϕ(β)=34β2[1βlg⁡1−β1+β+21−β2],β=vcdisplaystyle phi (beta )=frac 34beta ^2left[frac 1beta lg frac 1-beta 1+beta +frac 21-beta ^2right],;beta =frac vc,

Kaufmann noticed that the observed increase cannot be explained by this formula, so he separated the measured total mass into a mechanical (true) mass and an electromagnetic (apparent) mass, the mechanical mass being considerably greater than the electromagnetic one. However, he made two mistakes: As shown by Max Abraham, Kaufmann overlooked that Searle's formula only applies in the longitudinal direction, but for deflection measurements the formula for the transverse direction was important. Therefore, Abraham introduced the "transverse electromagnetic mass" with the following velocity dependence:

ϕ(β)=34β2(1+β22βlg⁡1+β1−β−1),displaystyle phi (beta )=frac 34beta ^2left(frac 1+beta ^22beta lg frac 1+beta 1-beta -1right),

Kaufmann also made a calculation mistake in deriving the deflection curves. Those errors were corrected by him in 1902.^[5]

In 1902 and 1903 Kaufmann performed another series of tests with updated and improved experimental techniques. The results were interpreted by him as a confirmation of Abraham's theory and of the assumption that the electron's mass is completely of electromagnetic origin.^[6][7]

Hermann Starke conducted similar measurements in 1903, although he used cathode rays limited to 0.3c. The results that he obtained were interpreted by him as being in agreement with those of Kaufmann.^[8]

Competing theories

Figure 3. Predictions of speed dependence of transverse electromagnetic mass according to the theories of Abraham, Lorentz, and Bucherer.

In 1902, Max Abraham published a theory based on the assumption that the electron was a rigid, perfect sphere, with its charge being distributed evenly on its surface. As explained above, he introduced the so-called "transverse electromagnetic mass" besides the "longitudinal electromagnetic mass", and argued that the entire electron mass is of electromagnetic origin.^{[A 6][A 7][9][10][11]}

Meanwhile, Lorentz (1899, 1904) extended his theory of electrons, assuming that an electron's charge was spread throughout its volume, and that in Kaufmann's experiment, its shape would be compressed in the direction of motion and would stay unchanged in the transverse directions. To Kaufmann's surprise, Lorentz could show that his model agreed with his experimental data as well. This model was further elaborated and perfected by Henri Poincaré (1905), so that Lorentz's theory was now in agreement with the principle of relativity.^{[A 8][A 9][12][13]}

A similar theory was developed by Alfred Bucherer and Paul Langevin in 1904, with the difference that the total volume occupied by the deformed electron was assumed unchanged. It turned out that this theory's prediction was closer to Abraham's theory than to Lorentz's.^{[A 10][14]}

Finally, Albert Einstein's theory of special relativity (1905) predicted the change of the point-like electron's mass due to the properties of the transformation between the rest-frame of the particle and the laboratory frame in which the measurements were performed. Mathematically, this calculation predicts the same dependence between velocity and mass as Lorentz's theory, although it assumes very different physical concepts.^{[A 11][15]}

As regards the increase of transverse electromagnetic mass, the predictions of the various theories were (Fig. 3):

Abrahamϕ(β)=34β2(1+β22βlg⁡1+β1−β−1)Lorentz--Einsteinϕ(β)=(1−β2)−1/2Bucherer--Langevinϕ(β)=(1−β2)−1/3displaystyle beginaligned&textAbraham&phi (beta )&=frac 34beta ^2left(frac 1+beta ^22beta lg frac 1+beta 1-beta -1right)\&textLorentz--Einstein&phi (beta )&=(1-beta ^2)^-1/2\&textBucherer--Langevin&phi (beta )&=(1-beta ^2)^-1/3endaligned

Experiments of 1905

In order to make a decision between those theories, Kaufmann again performed his experiments with higher precision. Kaufmann believed that he had conclusively disproven the formula of Lorentz–Einstein, and had therefore also disproven the principle of relativity. In his view, the only remaining options were between the theories of Abraham and Bucherer. Lorentz was perplexed and wrote that he was "at the end of his Latin".^{[A 12][A 13][16][17]}

However, criticism of Kaufmann's experiment arose.^{[A 14][A 15]} Shortly after Kaufmann published his results and the conclusions of his analysis, Max Planck decided to re-analyze the data obtained by the experiment. In 1906 and 1907, Planck published his own conclusion on the behavior of the inertial mass of electrons with high speeds. Using just nine data points from Kaufmann's publication in 1905, he recalculated the exact setup of the fields for each point, and compared the measurements against the predictions of the two competing theories. He showed that Kaufmann's results are not fully decisive and would lead to superluminal velocities.^[18][19]
Einstein remarked in 1907 that although Kaufmann's results were better in agreement with Abraham's and Bucherer's theories than with his own, the foundations of the other theories were not plausible and therefore had only little probability of being correct.^[20]

Subsequent experiments

Bucherer

Figure 4. Top view. Bucherer's experimental setup.

Figure 5. Cross-section through the axis of the circular capacitor at angle α with respect to the magnetic field H.

The main problem of Kaufmann's experiments was his use of parallel magnetic and electric fields, as pointed out by Adolf Bestelmeyer (1907). Using a method based on perpendicular magnetic and electric fields (introduced by J. J. Thomson and further developed to a velocity filter by Wilhelm Wien), Bestelmeyer obtained considerably different values for the charge-to-mass ratio for cathode rays up to 0.3c. However, Bestelmeyer added that his experiment was not precise enough to provide a definite decision between the theories.^[21]

Therefore, Alfred Bucherer (1908) conducted a precise measurement using a velocity filter similar to Bestelmeyer's. See Figs. 3 & 5. A radium beta source was placed at the center of a circular condenser consisting of two silvered glass plates spaced 0.25 mm apart and charged to about 500 volts, set in a homogeneous 140 Gauss magnetic field. The radium emitted beta rays in all directions, but in any particular direction α, only those beta rays exited the velocity filter whose speed was such that the electric and magnetic fields exactly compensated each other. After leaving the condenser, the rays were deflected by the magnetic field, and exposed a photographic plate set parallel to the condenser rim and perpendicular to the non-deflected rays.^[22][23]

Figure 6. Bucherer's data in five runs.

Figure 7. Wolz's data in 13 runs.

For his final analysis, Bucherer recalculated the measured values of five runs with Lorentz's and Abraham's formulas respectively, in order to obtain the charge-to-mass ratio as if the electrons were at rest. Since the ratio doesn't vary for resting electrons, the data points should be on a single horizontal line (see Fig. 6). However, this was approximately only in the case when the data were calculated with Lorentz's formula, while the results of Abraham's formula sharply deviated (the red and blue lines represent the average value according to both formulas). The agreement with the Lorentz–Einstein formula was interpreted by Bucherer as the confirmation of the relativity principle and the Lorentz–Einstein theory – a result immediately applauded by Lorentz, Einstein, and Hermann Minkowski.^{[A 16][A 17]}

In addition, Bucherer's apparatus was improved in 1909 by his student Kurt Wolz, who also obtained agreement with the Lorentz–Einstein formula (though he didn't compare Abraham's formula with his data, Fig. 7).^[24]

Even though many physicists accepted Bucherer's result, there still remained some doubts.^{[A 18][A 19]} For instance, Bestelmeyer published a paper in which he cast doubt on the validity of Bucherer's result. He argued that one experiment alone cannot establish the correctness of an important physical law, that Bucherer's result might be significantly distorted by non-compensated rays reaching the photographic plate, and that extensive data protocols and error analysis are necessary.^[25] A polemic dispute between those two scholars followed in a series of publications, in which Bestelmeyer argued that Wolz's experiments are affected by the same problems.^[26][27][28]

Hupka

Unlike Kaufmann and Bucherer, Karl Erich Hupka (1909) used cathode rays at 0.5c for his measurements. The radiation (generated at a copper cathode) was strongly accelerated by the field between cathode and anode in a highly evacuated discharge tube. The anode serving as a diaphragm was passed by the ray with constant velocity and drew the shadow image of two Wollaston wires on a phosphorescent screen behind a second diaphragm. If a current was generated behind this diaphragm, then the ray was deflected and the shadow image was displaced. The results were in agreement with Lorentz–Einstein, even though Hupka remarked that this experiment didn't represent a definitive result.^[29] Subsequently, W. Heil published some papers dealing with criticisms and interpretations of the result, to which Hupka replied.^[30][31][32]

Neumann and Guye/Lavanchy

Figure 8. Neumann's evaluation of 26 data points for each theory.

In 1914, Günther Neumann conducted new measurements using Bucherer's equipment, in particular making some improvements to address Bestelmeyer's criticisms, especially the question of non-compensated rays, and making extensive refinements to the data protocols. The calculation method was the same as Bucherer's (see Fig. 6). Also in this experiment, the data corresponding to Lorentz's formula are nearly on a horizontal line as required, while the data obtained from Abraham's formula sharply deviate (see Fig. 8). Neumann concluded that his experiments were in agreement with those of Bucherer and Hupka, definitely proving the Lorentz–Einstein formula in the range 0.4–0.7c, and refuted Abraham's formula. Instrumental uncertainties occurred in the range 0.7–0.8c, so the deviation from the Lorentz–Einstein formula in this range wasn't considered as being significant.^[33]

Figure 9. Guye and Lavanchy's evaluation of 25 data points for each theory.

In 1915, Charles-Eugène Guye and Charles Lavanchy measured the deflection of cathode rays at 0.25c–0.5c. They used a tube with a cathode and anode in order to accelerate the rays. A diaphragm at the anode produced a beam which was deflected. A screen was placed at the end of the apparatus, at which the impacts were photographed by a camera. They subsequently computated the ratio of transverse electromagnetic mass m_T and rest mass m₀ indicated by the red and blue curve, and obtained good agreement with the Lorentz–Einstein formula (see Fig. 9), supplementing Neumann's result.^[34][35]

Neumann's and Guye/Lavanchy's experiments were considered by many as conclusively proving the Lorentz-Einstein formula.^{[A 20][A 21][A 22]} Lorentz summarized these efforts in 1915:^{[A 23]}

Later experiments [..] have confirmed the formula [..] for the transverse electromagnetic mass, so that, in all probability, the only objection that could be raised against the hypothesis of the deformable electron and the principle of relativity has now been removed.

Further development

Figure 10. Rogers et al. electrostatic spectrograph

Zahn & Spees (1938)^[36] and Faragó & Lajos Jánossy (1954)^[37] argued that many assumptions employed in those early experiments as to the nature and the properties of electrons and the experimental setup, were wrong or imprecise. As with Kaufmann's experiments, the Bucherer–Neumann experiments would only show a qualitative increase of mass, and were incapable of deciding between the competing theories.^{[A 24][A 25]}

While the results of those electron deflection experiments were disputed for a long time, the investigations of the fine structure of the hydrogen lines by Karl Glitscher (based on the work of Arnold Sommerfeld) had already in 1917 provided a clear confirmation of the Lorentz–Einstein formula, because the relativistic expressions for momentum and energy were necessary to derive the fine structure, and a constituted a refutation of Abraham's theory.^{[38][A 26]}

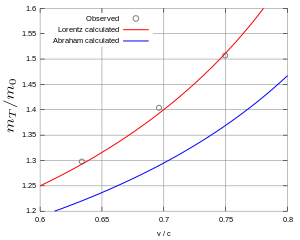
Figure 11. Three data points of Rogers et al., in agreement with the Lorentz–Einstein formula.

In addition, the first electron deflection experiments with sufficient precision was conducted by Rogers et al. (1940), who developed an improved setup. The radium decay series yields a spectrum of beta particles with a wide range of energies. The earlier measurements by Kaufmann, Bucherer, and others had used flat parallel plate condensers which provided no focusing of the beta particles. Rogers et al. (Fig. 10) instead constructed an electrostatic spectrograph capable of resolving the energy maxima of individual beta particle lines from the radium decay series. The electrostatic spectrograph was constructed of segments of two cylinders and was enclosed in an evacuated iron box. The beta rays were emitted from a fine platinum wire coated with radium active-deposit. The dispersed rays were incident on a slit in front of a Geiger counter. The data from this experiment was combined with previous magnetic spectrometer measurements of H_ρ to yield the charge-to-mass ratio, which was subsequently compared with the predictions of Lorentz and Abraham for the ratio of transverse mass and rest mass. The points were all on the curve representing the Lorentz–Einstein formula to within 1% (see Fig. 11).^[39] This experiment is seen as being sufficiently precise to distinguish between the theories.^{[A 27]}

Modern Tests

Since then, many additional experiments concerning the relativistic energy–momentum relation have been conducted, including measurements of the deflection of electrons, all of them confirming special relativity to high precision. Also in modern particle accelerators, the predictions of special relativity are routinely confirmed.

See also

• History of special relativity

References

Primary sources

Secondary sources

• 
  Battimelli, G. (1981). "The Electromagnetic Mass of the Electron: A Case Study of a Non-Crucial Experiment". Fundamenta Scientiae. 2: 137–150.
  


• 
  Janssen, Michel; Mecklenburg, Matthew (2007), "From classical to relativistic mechanics: Electromagnetic models of the electron", in V. F. Hendricks; et al., Interactions: Mathematics, Physics and Philosophy, Dordrecht: Springer, pp. 65–134
  

• 
  Lorentz, Hendrik Antoon (1916), The theory of electrons and its applications to the phenomena of light and radiant heat on the Internet Archive, Leipzig & Berlin: B.G. Teubner External link in |title= (help)
  

• 
  Miller, Arthur I. (1981), Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911), Reading: Addison–Wesley, ISBN 0-201-04679-2
  

• 
  Pais, Abraham (2005) [First published 1982], Subtle is the Lord: The Science and the Life of Albert Einstein, New York: Oxford University Press, ISBN 0-19-280672-6
  

• 
  Pauli, Wolfgang (1921), "Die Relativitätstheorie", Encyclopädie der mathematischen Wissenschaften, 5 (2): 539–776
  

In English: Pauli, W. (1981) [1921]. Theory of Relativity. Fundamental Theories of Physics. 165. Dover Publications. ISBN 0-486-64152-X.

• 
  Staley, Richard (2008), Einstein's generation, Chicago: University Press, ISBN 0-226-77057-5
  

External links

• 
  Presentation on Kaufmann experiment (PowerPoint)


• List of SR tests