Odtnhj

Foucault's pendulum in the Panthéon, Paris

Play media

Foucault Pendulum at COSI Columbus knocking over a ball

The Foucault pendulum (English: /fuːˈkoʊ/ foo-KOH; French pronunciation: ​[fuˈko]) or Foucault's pendulum is a simple device named after French physicist Léon Foucault and conceived as an experiment to demonstrate the Earth's rotation. The pendulum was introduced in 1851 and was the first experiment to give simple, direct evidence of the earth's rotation. Today, Foucault pendulums are popular displays in science museums and universities.^[1]

Original Foucault pendulum

Play media

Foucault's pendulum in the Panthéon, Paris

A Print of the Foucault Pendulum, 1895

The first public exhibition of a Foucault pendulum took place in February 1851 in the Meridian of the Paris Observatory. A few weeks later, Foucault made his most famous pendulum when he suspended a 28-kg brass-coated lead bob with a 67-m-long wire from the dome of the Panthéon, Paris. The plane of the pendulum's swing rotated clockwise approximately 11.3° per hour, making a full circle in approximately 31.8 hours. The original bob used in 1851 at the Panthéon was moved in 1855 to the Conservatoire des Arts et Métiers in Paris. A second temporary installation was made for the 50th anniversary in 1902.^[2]

During museum reconstruction in the 1990s, the original pendulum was temporarily displayed at the Panthéon (1995), but was later returned to the Musée des Arts et Métiers before it reopened in 2000.^[3] On April 6, 2010, the cable suspending the bob in the Musée des Arts et Métiers snapped, causing irreparable damage to the pendulum and to the marble flooring of the museum.^[4][5]

An exact copy of the original pendulum has been operating under the dome of the Panthéon, Paris since 1995.^[6]

Explanation of mechanics

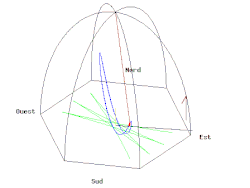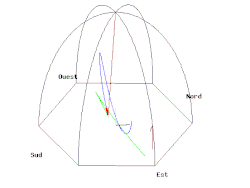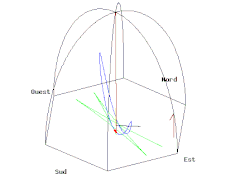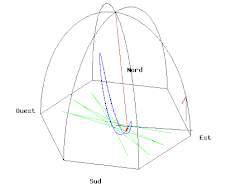
Animation of a Foucault pendulum at the Pantheon in Paris (48° 52' north), with the Earth's rotation rate greatly exaggerated. The green trace shows the path of the pendulum bob over the ground (a rotating reference frame), while in any vertical plane. The actual plane of swing appears to rotate relative to the Earth. The wire should be as long as possible—lengths of 12–30 m (39–98 ft) are common.^[7]

At either the North Pole or South Pole, the plane of oscillation of a pendulum remains fixed relative to the distant masses of the universe while Earth rotates underneath it, taking one sidereal day to complete a rotation. So, relative to Earth, the plane of oscillation of a pendulum at the North Pole – viewed from above – undergoes a full clockwise rotation during one day; a pendulum at the South Pole rotates counterclockwise.

When a Foucault pendulum is suspended at the equator, the plane of oscillation remains fixed relative to Earth. At other latitudes, the plane of oscillation precesses relative to Earth, but more slowly than at the pole; the angular speed, ω (measured in clockwise degrees per sidereal day), is proportional to the sine of the latitude, φdisplaystyle varphi :

ω=360∘sin⁡φ /daydisplaystyle omega =360^circ sin varphi /mathrm day ,

where latitudes north and south of the equator are defined as positive and negative, respectively. For example, a Foucault pendulum at 30° south latitude, viewed from above by an earthbound observer, rotates counterclockwise 360° in two days.

A Foucault pendulum at the North Pole: The pendulum swings in the same plane as the Earth rotates beneath it.

To demonstrate rotation directly rather than indirectly via the swinging pendulum, Foucault used a gyroscope in an 1852 experiment. The inner gimbal of the Foucault gyroscope was balanced on knife edge bearings on the outer gimbal and the outer gimbal was suspended by a fine, torsion-free thread in such a manner that the lower pivot point carried almost no weight. The gyro was spun to 9000–12000 revolutions per minute with an arrangement of gears before being placed into position, which was sufficient time to balance the gyroscope and carry out 10 minutes of experimentation. The instrument could be observed either with a microscope viewing a tenth of a degree scale or by a long pointer. At least three more copies of a Foucault gyro were made in convenient travelling and demonstration boxes and copies survive in the UK, France, and the US.

A Foucault pendulum requires care to set up because imprecise construction can cause additional veering which masks the terrestrial effect. The initial launch of the pendulum is critical; the traditional way to do this is to use a flame to burn through a thread which temporarily holds the bob in its starting position, thus avoiding unwanted sideways motion (see a detail of the launch at the 50th anniversary in 1902).

An excerpt from the illustrated supplement of the magazine Le Petit Parisien dated November 2, 1902, on the 50th anniversary of the experiment of Léon Foucault demonstrating the rotation of the earth.

Air resistance damps the oscillation, so some Foucault pendulums in museums incorporate an electromagnetic or other drive to keep the bob swinging; others are restarted regularly, sometimes with a launching ceremony as an added attraction.

The animation describes the motion of a Foucault pendulum at a latitude of 30°N. The plane of oscillation rotates by an angle of −180° during one day, so after two days, the plane returns to its original orientation.

A 'pendulum day' is the time needed for the plane of a freely suspended Foucault pendulum to complete an apparent rotation about the local vertical. This is one sidereal day divided by the sine of the latitude.^[8][9]

Precession as a form of parallel transport

Parallel transport of a vector around a closed loop on the sphere: The angle by which it twists, αdisplaystyle alpha , is proportional to the area inside the loop.

Graphs of precession period and precession per sidereal day vs latitude. The sign changes as a Foucault pendulum rotates anticlockwise in the Southern Hemisphere and clockwise in the Northern Hemisphere. The example shows that one in Paris precesses 271° each sidereal day, taking 31.8 hours per rotation.

In a near-inertial frame moving in tandem with Earth, but not sharing the rotation of the earth about its own axis, the suspension point of the pendulum traces out a circular path during one sidereal day.

At the latitude of Paris, 48 degrees 51 minutes north, a full precession cycle takes just under 32 hours, so after one sidereal day, when the Earth is back in the same orientation as one sidereal day before, the oscillation plane has turned by just over 270 degrees. If the plane of swing was north-south at the outset, it is east-west one sidereal day later.

This also implies that there has been exchange of momentum; the Earth and the pendulum bob have exchanged momentum. The Earth is so much more massive than the pendulum bob that the Earth's change of momentum is unnoticeable. Nonetheless, since the pendulum bob's plane of swing has shifted, the conservation laws imply that an exchange must have occurred.

Rather than tracking the change of momentum, the precession of the oscillation plane can efficiently be described as a case of parallel transport. For that, it can be demonstrated, by composing the infinitesimal rotations, that the precession rate is proportional to the projection of the angular velocity of Earth onto the normal direction to Earth, which implies that the trace of the plane of oscillation will undergo parallel transport. After 24 hours, the difference between initial and final orientations of the trace in the Earth frame is α = −2πsin(φ), which corresponds to the value given by the Gauss–Bonnet theorem. α is also called the holonomy or geometric phase of the pendulum. When analyzing earthbound motions, the Earth frame is not an inertial frame, but rotates about the local vertical at an effective rate of 2π sin(φ) radians per day. A simple method employing parallel transport within cones tangent to the Earth's surface can be used to describe the rotation angle of the swing plane of Foucault's pendulum.^[10][11]

From the perspective of an Earth-bound coordinate system with its x-axis pointing east and its y-axis pointing north, the precession of the pendulum is described by the Coriolis force. Consider a planar pendulum with natural frequency ω in the small angle approximation. There are two forces acting on the pendulum bob: the restoring force provided by gravity and the wire, and the Coriolis force. The Coriolis force at latitude φ is horizontal in the small angle approximation and is given by

Fc,x=2mΩdydtsin⁡(φ)Fc,y=−2mΩdxdtsin⁡(φ)displaystyle beginalignedF_c,x&=2mOmega dfrac dydtsin(varphi )\F_c,y&=-2mOmega dfrac dxdtsin(varphi )endaligned

where Ω is the rotational frequency of Earth, F_c,x is the component of the Coriolis force in the x-direction and F_c,y is the component of the Coriolis force in the y-direction.

The restoring force, in the small-angle approximation, is given by

Fg,x=−mω2xFg,y=−mω2y.displaystyle beginalignedF_g,x&=-momega ^2x\F_g,y&=-momega ^2y.endaligned

Using Newton's laws of motion this leads to the system of equations

d2xdt2=−ω2x+2Ωdydtsin⁡(φ)d2ydt2=−ω2y−2Ωdxdtsin⁡(φ).displaystyle beginaligneddfrac d^2xdt^2&=-omega ^2x+2Omega dfrac dydtsin(varphi )\dfrac d^2ydt^2&=-omega ^2y-2Omega dfrac dxdtsin(varphi ),.endaligned

Switching to complex coordinates z = x + iy, the equations read

d2zdt2+2iΩdzdtsin⁡(φ)+ω2z=0.displaystyle frac d^2zdt^2+2iOmega frac dzdtsin(varphi )+omega ^2z=0,.

To first order in Ω/ω this equation has the solution

z=e−iΩsin⁡(φ)t(c1eiωt+c2e−iωt).displaystyle z=e^-iOmega sin(varphi )tleft(c_1e^iomega t+c_2e^-iomega tright),.

If time is measured in days, then Ωt = 2π and the pendulum rotates by an angle of −2π sin(φ) during one day.

Foucault's Pendulum at the Ranchi Science Centre

Related physical systems

The device described by Wheatstone.

Many physical systems precess in a similar manner to a Foucault pendulum. As early as 1836, the Scottish mathematician Edward Sang contrived and explained the precession of a spinning top. In 1851, Charles Wheatstone
^[12] described an apparatus that consists of a vibrating spring that is mounted on top of a disk so that it makes a fixed angle ϕdisplaystyle phi with the disk. The spring is struck so that it oscillates in a plane. When the disk is turned, the plane of oscillation changes just like the one of a Foucault pendulum at latitude ϕdisplaystyle phi .

Similarly, consider a nonspinning, perfectly balanced bicycle wheel mounted on a disk so that its axis of rotation makes an angle ϕdisplaystyle phi with the disk. When the disk undergoes a full clockwise revolution, the bicycle wheel will not return to its original position, but will have undergone a net rotation of 2πsin⁡(ϕ)displaystyle 2pi ,sin(phi ).

Foucault-like precession is observed in a virtual system wherein a massless particle is constrained to remain on a rotating plane that is inclined with respect to the axis of rotation.^[13]

Spin of a relativistic particle moving in a circular orbit precesses similar to the swing plane of Foucault pendulum. The relativistic velocity space in Minkowski spacetime can be treated as a sphere S³ in 4-dimensional Euclidean space with imaginary radius and imaginary timelike coordinate. Parallel transport of polarization vectors along such sphere gives rise to Thomas precession, which is analogous to the rotation of the swing plane of Foucault pendulum due to parallel transport along a sphere S² in 3-dimensional Euclidean space.^[14]

In physics, the evolution of such systems is determined by geometric phases.^[15][16] Mathematically they are understood through parallel transport.

Foucault pendulums around the world

The Foucault pendulum at the California Academy of Sciences knocks over successive pegs as the Earth rotates

There are numerous Foucault pendulums at universities, science museums, and the like throughout the world. The United Nations headquarters in New York City has one; the largest is at the Oregon Convention Center.^[17][18]

South Pole

The experiment has also been carried out at the South Pole, where it was assumed that the rotation of the earth would have maximum effect^[19][20] at the Amundsen–Scott South Pole Station, in a six-story staircase of a new station under construction. The pendulum had a length of 33 m and the bob weighed 25 kg. The location was ideal: no moving air could disturb the pendulum, and the low viscosity of the cold air reduced air resistance. The researchers confirmed about 24 hours as the rotation period of the plane of oscillation.

See also

• Coriolis effect


• Earth's rotation


• Eötvös experiment


• Inertial frame


• Absolute rotation


• Lariat chain


• Precession

References

Further reading

• 
  Arnold, V.I. (1989). Mathematical Methods of Classical Mechanics. Springer. p. 123. ISBN 978-0-387-96890-2.
  


• 
  Marion, Jerry B.; Thornton, Stephen T. (1995). Classical dynamics of particles and systems (4th ed.). Brooks Cole. pp. 398–401. ISBN 978-0-03-097302-4.
  


• 
  Persson, Anders O. (2005). "The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885" (PDF). History of Meteorology. 2.
  

External links

Wikimedia Commons has media related to Foucault pendulums.

• 
  Rubin, Julian (2007). "The Invention of the Foucault Pendulum". Following the Path of Discovery, 2007, retrieved 2007-10-31. Directions for repeating Foucault's experiment, on amateur science site.


• Wolfe, Joe, "A derivation of the precession of the Foucault pendulum".


• "The Foucault Pendulum", derivation of the precession in polar coordinates.


• "The Foucault Pendulum" By Joe Wolfe, with film clip and animations.


• "Foucault's Pendulum" by Jens-Peer Kuska with Jeff Bryant, Wolfram Demonstrations Project: a computer model of the pendulum allowing manipulation of pendulum frequency, Earth rotation frequency, latitude, and time.


• "Webcam Kirchhoff-Institut für Physik, Universität Heidelberg".


• 
  California academy of sciences, CA Foucault pendulum explanation, in friendly format


• 
  Foucault pendulum model Exposition including a tabletop device that shows the Foucault effect in seconds.


• Foucault, M. L., Physical demonstration of the rotation of the Earth by means of the pendulum, Franklin Institute, 2000, retrieved 2007-10-31. Translation of his paper on Foucault pendulum.


• 
  Tobin, William. "The Life and Science of Léon Foucault".
  


• 
  Bowley, Roger (2010). "Foucault's Pendulum". Sixty Symbols. Brady Haran for University of Nottingham.
  


• 
  Foucault-inga Párizsban Foucault's Pendulum in Paris – video of the operating Foucault's Pendulum in the Panthéon (in Hungarian).


• 
  Pendolo nel Salone The Foucault Pendulum inside Palazzo della Ragione in Padova, Italy


• 
  MacMillan, William Duncan (1915). "On Foucault's Pendulum". Am. J. Math. 37 (1): 95–106. doi:10.2307/2370259. JSTOR 2370259.
  


• 
  Somerville, W. B. (1972). "The description of Foucault's pendulum". Q. J. Royal Astron. Soc. 13: 40–62. Bibcode:1972QJRAS..13...40S.
  


• 
  Braginsky, Vladimir B.; Polnarev, Aleksander G.; Thorne, Kip S. (1984). "Foucault Pendulum at the South Pole: Proposal For an Experiment to Detect the Earth's General Relativistic Gravitomagnetic Field". Phys. Rev. Lett. 53 (9): 863. Bibcode:1984PhRvL..53..863B. doi:10.1103/PhysRevLett.53.863.
  


• 
  Crane, H. Richard (1995). "Foucault pendulum "wall clock"". Am. J. Phys. 63 (1): 33–39. Bibcode:1995AmJPh..63...33C. doi:10.1119/1.17765.
  


• 
  Hard, John B.; Miller, Raymond E. (1998). "A simple geometric model for visualizing the motion of a Foucault pendulum". Am. J. Phys. 55 (1): 67. doi:10.119/1.14972 (inactive 2018-09-20).
  


• 
  Das, U.; Talukdar, B.; Shamanna, J. (2002). "Indirect Analytic Representation of Foucault's Pendulum". Czech. J. Phys. 52 (12): 1321–1327. Bibcode:2002CzJPh..52.1321D. doi:10.1023/A:1021819627736.
  


• 
  Salva, Horacio R.; Benavides, Rubén E.; Perez, Julio C.; Cuscueta, Diego J. (2010). "A Foucault's pendulum design". Rev. Sci. Instrum. 81 (11): 115102–115102–4. Bibcode:2010RScI...81k5102S. doi:10.1063/1.3494611. PMID 21133496.
  


• 
  Daliga, K.; Przyborski, M.; Szulwic, J. (2015). "Foucault's Pendulum. Uncomplicated Tool in the Study of Geodesy and Cartography". EDULEARN15 Proceedings - 7th International Conference on Education and New Learning Technologies, Barcelona, Spain. ISBN 978-84-606-8243-1.