Odtnhj

Acceleration
In the absence of air resistance and thus terminal velocity, a falling ball would continue to accelerate.
Common symbols	a
SI unit	m/s2, m·s−2, m s−2
Dimension	L T -2

Part of a series of articles about
Classical mechanics
F→=ma→displaystyle vec F=mvec a Second law of motion
History Timeline
Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Udwadia–Kalaba equation Koopman–von Neumann mechanics
Core topics Damping (ratio) Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Mechanics of planar particle motion Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational speed Angular acceleration / displacement / frequency / velocity
Scientists Galileo Huygens Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy
v t e

In physics, acceleration is the rate of change of velocity of an object with respect to time. An object's acceleration is the net result of all forces acting on the object, as described by Newton's Second Law.^[1] The SI unit for acceleration is metre per second squared (m s⁻²). Accelerations are vector quantities (they have magnitude and direction) and add according to the parallelogram law.^[2][3] The vector of the net force acting on a body has the same direction as the vector of the body's acceleration, and its magnitude is proportional to the magnitude of the acceleration, with the object's mass (a scalar quantity) as proportionality constant.

For example, when a car starts from a standstill (zero velocity, in an inertial frame of reference) and travels in a straight line at increasing speeds, it is accelerating in the direction of travel. If the car turns, an acceleration occurs toward the new direction. The forward acceleration of the car is called a linear (or tangential) acceleration, the reaction to which passengers in the car experience as a force pushing them back into their seats. When changing direction, this is called radial (as orthogonal to tangential) acceleration, the reaction to which passengers experience as a sideways force. If the speed of the car decreases, this is an acceleration in the opposite direction of the velocity of the vehicle, sometimes called deceleration.^[4] Passengers experience the reaction to deceleration as a force pushing them forwards. Both acceleration and deceleration are treated the same, they are both changes in velocity. Each of these accelerations (tangential, radial, deceleration) is felt by passengers until their velocity (speed and direction) matches that of the uniformly moving car.

Definition and properties

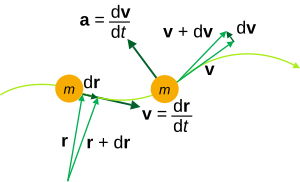
Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a.

Average acceleration

Acceleration is the rate of change of velocity. At any point on a trajectory, the magnitude of the acceleration is given by the rate of change of velocity in both magnitude and direction at that point. The true acceleration at time t is found in the limit as time interval Δt → 0 of Δv/Δt

An object's average acceleration over a period of time is its change in velocity (Δv)displaystyle (Delta mathbf v ) divided by the duration of the period (Δt)displaystyle (Delta t). Mathematically,

a¯=ΔvΔt.displaystyle bar mathbf a =frac Delta mathbf v Delta t.

Instantaneous acceleration

From bottom to top:

• an acceleration function a(t);


• the integral of the acceleration is the velocity function v(t);


• and the integral of the velocity is the distance function s(t).

Instantaneous acceleration, meanwhile, is the limit of the average acceleration over an infinitesimal interval of time. In the terms of calculus, instantaneous acceleration is the derivative of the velocity vector with respect to time:

a=limΔt→0ΔvΔt=dvdtdisplaystyle mathbf a =lim _Delta tto 0frac Delta mathbf v Delta t=frac dmathbf v dt

(Here and elsewhere, if motion is in a straight line, vector quantities can be substituted by scalars in the equations.)

It can be seen that the integral of the acceleration function a(t) is the velocity function v(t); that is, the area under the curve of an acceleration vs. time (a vs. t) graph corresponds to velocity.

v=∫a dtdisplaystyle mathbf v =int mathbf a dt

As acceleration is defined as the derivative of velocity, v, with respect to time t and velocity is defined as the derivative of position, x, with respect to time, acceleration can be thought of as the second derivative of x with respect to t:

a=dvdt=d2xdt2displaystyle mathbf a =frac dmathbf v dt=frac d^2mathbf x dt^2

Units

Acceleration has the dimensions of velocity (L/T) divided by time, i.e. L.T⁻². The SI unit of acceleration is the metre per second squared (m s⁻²); or "metre per second per second", as the velocity in metres per second changes by the acceleration value, every second.

Other forms

An object moving in a circular motion—such as a satellite orbiting the Earth—is accelerating due to the change of direction of motion, although its speed may be constant. In this case it is said to be undergoing centripetal (directed towards the center) acceleration.

Proper acceleration, the acceleration of a body relative to a free-fall condition, is measured by an instrument called an accelerometer.

In classical mechanics, for a body with constant mass, the (vector) acceleration of the body's center of mass is proportional to the net force vector (i.e. sum of all forces) acting on it (Newton's second law):

F=ma→a=F/mdisplaystyle mathbf F =mmathbf a quad to quad mathbf a =mathbf F /m

where F is the net force acting on the body, m is the mass of the body, and a is the center-of-mass acceleration. As speeds approach the speed of light, relativistic effects become increasingly large.

Tangential and centripetal acceleration

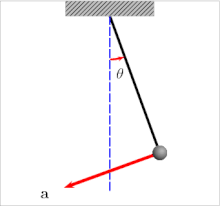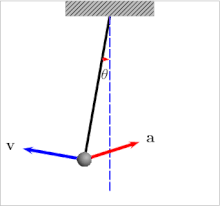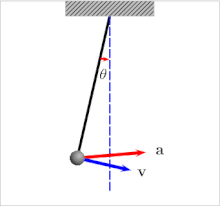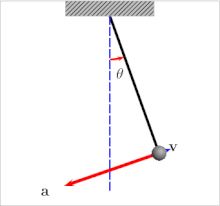
An oscillating pendulum, with velocity and acceleration marked. It experiences both tangential and centripetal acceleration.

Components of acceleration for a curved motion. The tangential component a_t is due to the change in speed of traversal, and points along the curve in the direction of the velocity vector (or in the opposite direction). The normal component (also called centripetal component for circular motion) a_c is due to the change in direction of the velocity vector and is normal to the trajectory, pointing toward the center of curvature of the path.

The velocity of a particle moving on a curved path as a function of time can be written as:

v(t)=v(t)v(t)v(t)=v(t)ut(t),displaystyle mathbf v (t)=v(t)frac mathbf v (t)v(t)=v(t)mathbf u _mathrm t (t),

with v(t) equal to the speed of travel along the path, and

ut=v(t)v(t) ,displaystyle mathbf u _mathrm t =frac mathbf v (t)v(t) ,

a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of u_t, the acceleration of a particle moving on a curved path can be written using the chain rule of differentiation^[5] for the product of two functions of time as:

a=dvdt=dvdtut+v(t)dutdt=dvdtut+v2run ,displaystyle beginalignedat3mathbf a &=frac mathrm d mathbf v mathrm d t\&=frac mathrm d vmathrm d tmathbf u _mathrm t +v(t)frac dmathbf u _mathrm t dt\&=frac mathrm d vmathrm d tmathbf u _mathrm t +frac v^2rmathbf u _mathrm n ,\endalignedat

where u_n is the unit (inward) normal vector to the particle's trajectory (also called the principal normal), and r is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the normal or radial acceleration (or centripetal acceleration in circular motion, see also circular motion and centripetal force).

Geometrical analysis of three-dimensional space curves, which explains tangent, (principal) normal and binormal, is described by the Frenet–Serret formulas.^[6][7]

Special cases

Uniform acceleration

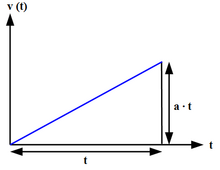
Calculation of the speed difference for a uniform acceleration

Uniform or constant acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.

A frequently cited example of uniform acceleration is that of an object in free fall in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field strength g (also called acceleration due to gravity). By Newton's Second Law the force, F, acting on a body is given by:

F=mgdisplaystyle mathbf F =mmathbf g

Because of the simple analytic properties of the case of constant acceleration, there are simple formulas relating the displacement, initial and time-dependent velocities, and acceleration to the time elapsed:^[8]

s(t)=s0+v0t+12at2=s0+v0+v(t)2tdisplaystyle mathbf s (t)=mathbf s _0+mathbf v _0t+tfrac 12mathbf a t^2=mathbf s _0+frac mathbf v _0+mathbf v (t)2t

v(t)=v0+atdisplaystyle mathbf v (t)=mathbf v _0+mathbf a t

v2(t)=v02+2a⋅[s(t)−s0]displaystyle v^2(t)=v_0^2+2mathbf acdot [mathbf s (t)-mathbf s _0]

where

• 
  tdisplaystyle t is the elapsed time,


• 
  s0displaystyle mathbf s _0 is the initial displacement from the origin,


• 
  s(t)displaystyle mathbf s (t) is the displacement from the origin at time tdisplaystyle t,


• 
  v0displaystyle mathbf v _0 is the initial velocity,


• 
  v(t)displaystyle mathbf v (t) is the velocity at time tdisplaystyle t, and


• 
  adisplaystyle mathbf a is the uniform rate of acceleration.

In particular, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, which describes, e. g., the trajectory of a projectile in a vacuum near the surface of Earth.^[9]

Circular motion

Position vector r, always points radially from the origin.

Velocity vector v, always tangent to the path of motion.

Acceleration vector a, not parallel to the radial motion but offset by the angular and Coriolis accelerations, nor tangent to the path but offset by the centripetal and radial accelerations.

Kinematic vectors in plane polar coordinates. Notice the setup is not restricted to 2d space, but may represent the osculating plane plane in a point of an arbitrary curve in any higher dimension.

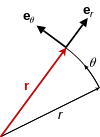
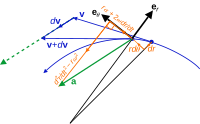
In uniform circular motion, that is moving with constant speed along a circular path, a particle experiences an acceleration resulting from the change of the direction of the velocity vector, while its magnitude remains constant. The derivative of the location of a point on a curve with respect to time, i.e. its velocity, turns out to be always exactly tangential to the curve, respectively orthogonal to the radius in this point. Since in uniform motion the velocity in the tangential direction does not change, the acceleration must be in radial direction, pointing to the center of the circle. This acceleration constantly changes the direction of the velocity to be tangent in the neighboring point, thereby rotating the velocity vector along the circle. For a given speed vdisplaystyle v, the magnitude of this geometrically caused acceleration is inversely proportional to the radius rdisplaystyle r of the circle, and increases as the square of this speed:

a=v2⋅1r.displaystyle textrm a=v^2cdot frac 1r;.

Expressing this vector in polar components, where rdisplaystyle mathbf r is a vector from the centre of the circle to the particle with magnitude equal to this distance, and considering the orientation of the acceleration towards the center, yields

a=−v2|r|⋅r|r|.displaystyle mathbf a =-frac v^2cdot frac mathbf r ;.

As usual in rotations, the speed vdisplaystyle v of a particle may be expressed as an angular speed with respect to a point at the distance rdisplaystyle r as

ω=vr.displaystyle omega =frac vr.

Thus a=−ω2r.displaystyle mathbf a =-omega ^2mathbf r ;.

This acceleration and the mass of the particle determine the necessary centripetal force, directed toward the centre of the circle, as the net force acting on this particle to keep it in this uniform circular motion. The so-called 'centrifugal force', appearing to act outward on the body, is a so called pseudo force experienced in the frame of reference of the body in circular motion, due to the body's linear momentum, a vector tangent to the circle of motion.

In a nonuniform circular motion, i.e., the speed along the curved path is changing, the acceleration has a non-zero component tangential to the curve, and is not confined to the principal normal, which directs to the center of the osculating circle, that determines the radius rdisplaystyle r for the centripetal acceleration. The tangential component is given by the angular acceleration αdisplaystyle alpha , i.e., the rate of change α=ω˙displaystyle alpha =dot omega of the angular speed ωdisplaystyle omega times the radius rdisplaystyle r. That is,

a=rα.displaystyle a=ralpha .

The sign of the tangential component of the acceleration is determined by the sign of the angular acceleration (αdisplaystyle alpha ), and the tangent is of course always directed at right angles to the radius vector.

Relation to relativity

Special relativity

The special theory of relativity describes the behavior of objects traveling relative to other objects at speeds approaching that of light in a vacuum. Newtonian mechanics is exactly revealed to be an approximation to reality, valid to great accuracy at lower speeds. As the relevant speeds increase toward the speed of light, acceleration no longer follows classical equations.

As speeds approach that of light, the acceleration produced by a given force decreases, becoming infinitesimally small as light speed is approached; an object with mass can approach this speed asymptotically, but never reach it.

General relativity

Unless the state of motion of an object is known, it is impossible to distinguish whether an observed force is due to gravity or to acceleration—gravity and inertial acceleration have identical effects. Albert Einstein called this the equivalence principle, and said that only observers who feel no force at all—including the force of gravity—are justified in concluding that they are not accelerating.^[10]

Conversions

See also

References

External links

Wikimedia Commons has media related to Acceleration.

• 
  Acceleration Calculator Simple acceleration unit converter


• 
  Measurespeed.com - Acceleration Calculator Based on starting & ending speed and time elapsed.