Odtnhj

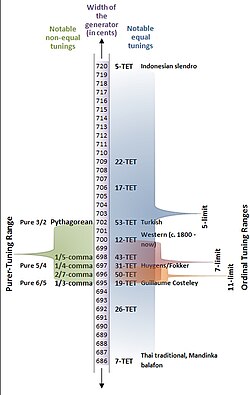
Figure 1: 31-ET on the regular diatonic tuning continuum at P5= 696.77 cents, from (Milne et al. 2007).^[1]

In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET, 31-EDO (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equal-sized steps (equal frequency ratios). Play (help·info) Each step represents a frequency ratio of ³¹√2, or 38.71 cents (Play (help·info)).

31-ET is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in 31-ET is precisely the same as it is in any other syntonic tuning (such as 12-ET), so long as the notes are spelled properly — that is, with no assumption of enharmonicity.

History and use

Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis — the ratio of an octave to three major thirds, 128:125 or 41.06 cents — was approximately a fifth of a tone and a third of a semitone. In 1555, Nicola Vincento proposed an extended-meantone tuning of 31 tones. In 1666, Lemme Rossi first proposed an equal temperament of this order. In 1691, having discovered it independently, scientist Christiaan Huygens wrote about it also.^[2] Since the standard system of tuning at that time was quarter-comma meantone, in which the fifth is tuned to ⁴√5, the appeal of this method was immediate, as the fifth of 31-ET, at 696.77 cents, is only 0.19 cent wider than the fifth of quarter-comma meantone. Huygens not only realized this, he went farther and noted that 31-ET provides an excellent approximation of septimal, or 7-limit harmony. In the twentieth century, physicist, music theorist and composer Adriaan Fokker, after reading Huygens's work, led a revival of interest in this system of tuning which led to a number of compositions, particularly by Dutch composers. Fokker designed the Fokker organ, a 31-tone equal-tempered organ, which was installed in Teyler's Museum in Haarlem in 1951 and moved to Muziekgebouw aan 't IJ in 2010 where it has been frequently used in concerts since it moved.

Interval size

Here are the sizes of some common intervals:

interval name	size (steps)	size (cents)	midi	just ratio	just (cents)	midi	error
octave	31	1200		2:1	1200		0
harmonic seventh	25	967.74	Play (help·info)	7:4	968.83	Play (help·info)	−01.09
perfect fifth	18	696.77	Play (help·info)	3:2	701.96	Play (help·info)	−05.19
greater septimal tritone	16	619.35		10:70	617.49		+01.87
lesser septimal tritone	15	580.65	Play (help·info)	7:5	582.51	Play (help·info)	−01.86
undecimal tritone, 11th harmonic	14	541.94	Play (help·info)	11:80	551.32	Play (help·info)	−09.38
perfect fourth	13	503.23	Play (help·info)	4:3	498.04	Play (help·info)	+05.19
septimal narrow fourth	12	464.52	Play (help·info)	21:16	470.78	Play (help·info)	−06.26
tridecimal augmented third, and greater major third	12	464.52	Play (help·info)	13:10	454.21	Play (help·info)	+10.31
septimal major third	11	425.81	Play (help·info)	9:7	435.08	Play (help·info)	−09.27
undecimal major third	11	425.81	Play (help·info)	14:11	417.51	Play (help·info)	+08.30
major third	10	387.10	Play (help·info)	5:4	386.31	Play (help·info)	+00.79
tridecimal neutral third	09	348.39	Play (help·info)	16:13	359.47	Play (help·info)	−11.09
undecimal neutral third	09	348.39	Play (help·info)	11:90	347.41	Play (help·info)	+00.98
minor third	08	309.68	Play (help·info)	6:5	315.64	Play (help·info)	−05.96
septimal minor third	07	270.97	Play (help·info)	7:6	266.87	Play (help·info)	+04.10
septimal whole tone	06	232.26	Play (help·info)	8:7	231.17	Play (help·info)	+01.09
whole tone, major tone	05	193.55	Play (help·info)	9:8	203.91	Play (help·info)	−10.36
whole tone, minor tone	05	193.55	Play (help·info)	10:90	182.40	Play (help·info)	+11.15
greater undecimal neutral second	04	154.84	Play (help·info)	11:10	165.00		−10.16
lesser undecimal neutral second	04	154.84	Play (help·info)	12:11	150.64	Play (help·info)	+04.20
septimal diatonic semitone	03	116.13	Play (help·info)	15:14	119.44	Play (help·info)	−03.31
diatonic semitone, just	03	116.13	Play (help·info)	16:15	111.73	Play (help·info)	+04.40
septimal chromatic semitone	02	077.42	Play (help·info)	21:20	084.47	Play (help·info)	−07.05
chromatic semitone, Just	02	077.42	Play (help·info)	25:24	070.67	Play (help·info)	+06.75
lesser diesis	01	038.71	Play (help·info)	128:125	041.06	Play (help·info)	−02.35
undecimal diesis	01	038.71	Play (help·info)	45:44	038.91	Play (help·info)	−00.20
septimal diesis	01	038.71	Play (help·info)	49:48	035.70	Play (help·info)	+03.01

The 31 equal temperament has a very close fit to the 7:6, 8:7, and 7:5 ratios, which have no approximate fits in 12 equal temperament and only poor fits in 19 equal temperament. The composer Joel Mandelbaum (born 1932) used this tuning system specifically because of its good matches to the 7th and 11th partials in the harmonic series.^[3] The tuning has poor matches to both the 9:8 and 10:9 intervals (major and minor tone in just intonation); however, it has a good match for the average of the two. Practically it is very close to quarter-comma meantone.

This tuning can be considered a meantone temperament. It has the necessary property that a chain of its four fifths is equivalent to its major third (the syntonic comma 81:80 is tempered out), which also means that it contains a "meantone" that falls between the sizes of 10:9 and 9:8 as the combination of one of each of its chromatic and diatonic semitones.

Scale diagram

The following are the 31 notes in the scale:

Interval (cents)		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39
Note name	A		B		A♯		B♭		A		B		C♭		B♯		C		D		C♯		D♭		C		D		E		D♯		E♭		D		E		F♭		E♯		F		G		F♯		G♭		F		G		A		G♯		A♭		G		A
Note (cents)	0		39		77		116		154		194		232		271		310		348		387		426		465		503		542		581		619		658		697		735		774		813		852		890		929		968		1006		1045		1084		1123		1161		1200

The five "double flat" notes and five "double sharp" notes may be replaced by half sharps and half flats, similar to the quarter tone system:

Interval (cents)		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39		39
Note name	A		A		A♯		B♭		B		B		C♭		B♯		C		C		C♯		D♭		D		D		D		D♯		E♭		E		E		F♭		E♯		F		F		F♯		G♭		G		G		G		G♯		A♭		A		A
Note (cents)	0		39		77		116		154		194		232		271		310		348		387		426		465		503		542		581		619		658		697		735		774		813		852		890		929		968		1006		1045		1084		1123		1161		1200

Circle of fifths in 31 equal temperament

Key Signature								Number of Sharps	Key Signature								Number of Flats
C Major	C	D	E	F	G	A	B	0
G Major	G	A	B	C	D	E	F♯	1
D Major	D	E	F♯	G	A	B	C♯	2
A Major	A	B	C♯	D	E	F♯	G#	3
E Major	E	F♯	G♯	A	B	C♯	D♯	4
B Major	B	C♯	D♯	E	F♯	G♯	A♯	5
F♯ Major	F♯	G♯	A♯	B	C♯	D♯	E♯	6
C♯ Major	C♯	D♯	E♯	F♯	G♯	A♯	B♯	7
G♯Major	G♯	A♯	B♯	C♯	D♯	E♯	F𝄪	8
D♯ Major	D♯	E♯	F𝄪	G♯	A♯	B♯	C𝄪	9
A♯ Major	A♯	B♯	C𝄪	D♯	E♯	F𝄪	G𝄪	10	C𝄫♭Major	C𝄫♭	D𝄫♭	E𝄫♭	F𝄫♭	G𝄫♭	A𝄫♭	B𝄫♭	21
E♯ Major	E♯	F𝄪	G𝄪	A♯	B♯	C𝄪	D𝄪	11	G𝄫♭ Major	G𝄫♭	A𝄫♭	B𝄫♭	C𝄫♭	D𝄫♭	E𝄫♭	F𝄫	20
B♯ Major	B♯	C𝄪	D𝄪	E♯	F𝄪	G𝄪	A𝄪	12	D𝄫♭ Major	D𝄫♭	E𝄫♭	F𝄫	G𝄫♭	A𝄫♭	B𝄫♭	C𝄫	19
F𝄪 Major	F𝄪	G𝄪	A𝄪	B♯	C𝄪	D𝄪	E𝄪	13	A𝄫♭ Major	A𝄫♭	B𝄫♭	C𝄫	D𝄫♭	E𝄫♭	F𝄫	G𝄫	18
C𝄪 Major	C𝄪	D𝄪	E𝄪	F𝄪	G𝄪	A𝄪	B𝄪	14	E𝄫♭ Major	E𝄫♭	F𝄫	G𝄫	A𝄫♭	B𝄫♭	C𝄫	D𝄫	17
G𝄪 Major	G𝄪	A𝄪	B𝄪	C𝄪	D𝄪	E𝄪	F♯𝄪	15	B𝄫♭ Major	B𝄫♭	C𝄫	D𝄫	E𝄫♭	F𝄫	G𝄫	A𝄫	16
D𝄪 Major	D𝄪	E𝄪	F♯𝄪	G𝄪	A𝄪	B𝄪	C♯𝄪	16	F𝄫 Major	F𝄫	G𝄫	A𝄫	B𝄫♭	C𝄫	D𝄫	E𝄫	15
A𝄪 Major	A𝄪	B𝄪	C♯𝄪	D𝄪	E𝄪	F♯𝄪	G♯𝄪	17	C𝄫 Major	C𝄫	D𝄫	E𝄫	F𝄫	G𝄫	A𝄫	B𝄫	14
E𝄪 Major	E𝄪	F♯𝄪	G♯𝄪	A𝄪	B𝄪	C♯𝄪	D♯𝄪	18	G𝄫 Major	G𝄫	A𝄫	B𝄫	C𝄫	D𝄫	E𝄫	F♭	13
B𝄪 Major	B𝄪	C♯𝄪	D♯𝄪	E𝄪	F♯𝄪	G♯𝄪	A♯𝄪	19	D𝄫 Major	D𝄫	E𝄫	F♭	G𝄫	A𝄫	B𝄫	C♭	12
F♯𝄪 Major	F♯𝄪	G♯𝄪	A♯𝄪	B𝄪	C♯𝄪	D♯𝄪	E♯𝄪	20	A𝄫 Major	A𝄫	B𝄫	C♭	D𝄫	E𝄫	F♭	G♭	11
C♯𝄪 Major	C♯𝄪	D♯𝄪	E♯𝄪	F♯𝄪	G♯𝄪	A♯𝄪	B♯𝄪	21	E𝄫 Major	E𝄫	F♭	G♭	A𝄫	B𝄫	C♭	D♭	10
									B𝄫 Major	B𝄫	C♭	D♭	E𝄫	F♭	G♭	A♭	9
									F♭ Major	F♭	G♭	A♭	B𝄫	C♭	D♭	E♭	8
									C♭ Major	C♭	D♭	E♭	F♭	G♭	A♭	B♭	7
									G♭ Major	G♭	A♭	B♭	C♭	D♭	E♭	F	6
									D♭ Major	D♭	E♭	F	G♭	A♭	B♭	C	5
									A♭ Major	A♭	B♭	C	D♭	E♭	F	G	4
									E♭ Major	E♭	F	G	A♭	B♭	C	D	3
									B♭ Major	B♭	C	D	E♭	F	G	A	2
									F Major	F	G	A	B♭	C	D	E	1
									C Major	C	D	E	F	G	A	B	0

Chords of 31 equal temperament

Many chords of 31-ET are discussed in the article on septimal meantone temperament. Chords not discussed there include the neutral thirds triad (Play (help·info)), which might be written C–E–G, C–D–G or C–F–G, and the Orwell tetrad, which is C–E–F–B.

I–IV–V–I chord progression in 31 tone equal temperament.^[4]

Play (help·info) Whereas in 12TET B♮ is 11 steps, in 31-TET B♮ is 28 steps.

C subminor, C minor, C major, C supermajor (topped by A♭) in 31 equal temperament

Usual chords like the major chord are rendered nicely in 31-ET because the third and the fifth are very well approximated. Also, it is possible to play subminor chords (where the first third is subminor) and supermajor chords (where the first third is supermajor).

C major seventh and G minor, twice in 31 equal temperament, then twice in 12 equal temperament

It is also possible to render nicely the harmonic seventh chord. For example on C with C–E–G–A♯. The seventh here is different from stacking a fifth and a minor third, which instead yields B♭ to make a dominant seventh. This difference cannot be made in 12-ET.

References

^ Milne, A., Sethares, W.A. and Plamondon, J., "Isomorphic Controllers and Dynamic Tuning: Invariant Fingerings Across a Tuning Continuum", Computer Music Journal, Winter 2007, Vol. 31, No. 4, Pages 15-32.

^ Monzo, Joe (2005). "Equal-Temperament". Tonalsoft Encyclopedia of Microtonal Music Theory. Joe Monzo. Retrieved 28 February 2019..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

^ Keislar, Douglas. "Six American Composers on Nonstandard Tunnings: Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt", Perspectives of New Music, Vol. 29, No. 1. (Winter, 1991), pp. 176-211.

^ Andrew Milne, William Sethares, and James Plamondon (2007). "Isomorphic Controllers and Dynamic Tuning: Invariant Fingering over a Tuning Continuum", p.29. Computer Music Journal, 31:4, pp.15–32, Winter 2007.

External links

The Huygens Fokker foundation for micro-tonal music, in Dutch and English

Fokker, Adriaan Daniël, Equal Temperament and the Thirty-one-keyed organ

Rapoport, Paul, About 31-tone Equal Temperament

Terpstra, Siemen, Toward a Theory of Meantone (and 31-et) Harmony

Barbieri, Patrizio. Enharmonic instruments and music, 1470-1900. (2008) Latina, Il Levante Libreria Editrice

M. Khramov, “Approximation to 7-Limit Just Intonation in a Scale of 31EDO,” Proceedings of the FRSM-2009 International Symposium Frontiers of Research on Speech and Music, pp. 73–82, ABV IIITM, Gwalior, 2009.

31 Tone Equal Temperament

[1] Milne, A., Sethares, W.A. and Plamondon, J., "Isomorphic Controllers and Dynamic Tuning: Invariant Fingerings Across a Tuning Continuum", Computer Music Journal, Winter 2007, Vol. 31, No. 4, Pages 15-32.

[2] Monzo, Joe (2005). "Equal-Temperament". Tonalsoft Encyclopedia of Microtonal Music Theory. Joe Monzo. Retrieved 28 February 2019..mw-parser-output cite.citationfont-style:inherit.mw-parser-output .citation qquotes:"""""""'""'".mw-parser-output .citation .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .citation .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-ws-icon abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center.mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-maintdisplay:none;color:#33aa33;margin-left:0.3em.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em

[3] Keislar, Douglas. "Six American Composers on Nonstandard Tunnings: Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt", Perspectives of New Music, Vol. 29, No. 1. (Winter, 1991), pp. 176-211.

[4] Andrew Milne, William Sethares, and James Plamondon (2007). "Isomorphic Controllers and Dynamic Tuning: Invariant Fingering over a Tuning Continuum", p.29. Computer Music Journal, 31:4, pp.15–32, Winter 2007.

v t e Christiaan Huygens
Books	Systema Saturnium (1659) De Vi Centrifiga (1659) Horologium Oscillatorium (1673) Traité de la Lumiére (1692) Cosmotheoros (1698)
In science and natural philosophy	Centripetal acceleration Coupled oscillation Conception of the standardization of the temperature scale Early history of classical mechanics Early history of calculus Huygens' law Huygens' lemniscate Huygens' principle (Huygens–Fresnel principle) Huygens' construction Huygens' tritone Huygens' wavelet Huygens' wave theory Huygens–Steiner theorem Hypothesis of intelligent extraterrestrial life Isochrone curve (tautochrone curve) Foundations of differential geometry of curves (mathematical notions of the evolute and involute of the curve) Scientific foundations of horology Mathematical and physical investigations of properties of the pendulum Modern conception of centrifugal and centripetal forces Music theory of microtones (31 equal temperament) Polarization of light (Iceland spar) Rings of Saturn Titan (moon) Theoretical foundations of wave optics (wave theory of light)
In technology	Inventions by Huygens Aerial telescope Centrifugal governor Cycloidal pendulum Huygens' engine .mw-parser-output .noitalicfont-style:normal ¹ Huygens' eyepiece Magic lantern ² Spiral balance spring Precision timekeeping (pendulum clock and spiral-hairspring watch)
Recognitions	List of things named after Christiaan Huygens 2801 Huygens Cassini–Huygens Huygens probe Mons Huygens Huygens (crater) Huygens-Fokker Foundation Huygens Gap Huygens Ringlet Horologium (constellation)
Other topics	Cosmos: A Personal Voyage - Episode 6: "Travellers' Tales" (1980 documentary TV series by Carl Sagan) Clocks and Culture, 1300–1700 (1967 history book by Carlo Cipolla) Revolution in Time: Clocks and the Making of the Modern World (1983 history book by David Landes) Scientific Revolution Golden Age of Dutch science and technology Science and technology in the Dutch Republic Académie des Sciences
Related people	Huygens family Galileo Galilei René Descartes Salomon Coster Antonie van Leeuwenhoek Gottfried Wilhelm Leibniz Isaac Newton Robert Hooke Denis Papin Augustin-Jean Fresnel Thomas Young
¹ A rudimentary prototype of internal combustion piston engine. ² An early practical type of image projector and a precursor to both the modern slide projector and the movie projector. Wikiquote Wikisource texts

搜尋此網誌

Odtnhj

31 equal temperament

Contents

History and use

Interval size

Scale diagram

Chords of 31 equal temperament

See also

References

External links

這個網誌中的熱門文章

Barbados

How to read a connectionString WITH PROVIDER in .NET Core?

Node.js Script on GitHub Pages or Amazon S3