Odtnhj

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector that gives the displacement of the one point from the other.

Informal description

A pictorial representation of the tangent space of a single point xdisplaystyle x on a sphere. A vector in this tangent space represents a possible velocity at xdisplaystyle x. After moving in that direction to a nearby point, the velocity would then be given by a vector in the tangent space of that point—a different tangent space that is not shown.

In differential geometry, one can attach to every point xdisplaystyle x of a differentiable manifold a tangent space—a real vector space that intuitively contains the possible directions in which one can tangentially pass through xdisplaystyle x. The elements of the tangent space at xdisplaystyle x are called the tangent vectors at xdisplaystyle x. This is a generalization of the notion of a bound vector in a Euclidean space. The dimension of the tangent space at every point of a connected manifold is the same as that of the manifold itself.

For example, if the given manifold is a 2displaystyle 2-sphere, then one can picture the tangent space at a point as the plane that touches the sphere at that point and is perpendicular to the sphere's radius through the point. More generally, if a given manifold is thought of as an embedded submanifold of Euclidean space, then one can picture a tangent space in this literal fashion. This was the traditional approach toward defining parallel transport and was used by Dirac.^[1] More strictly, this defines an affine tangent space, which is distinct from the space of tangent vectors described by modern terminology.

In algebraic geometry, in contrast, there is an intrinsic definition of the tangent space at a point of an algebraic variety Vdisplaystyle V that gives a vector space with dimension at least that of Vdisplaystyle V itself. The points pdisplaystyle p at which the dimension of the tangent space is exactly that of Vdisplaystyle V are called non-singular points; the others are called singular points. For example, a curve that crosses itself does not have a unique tangent line at that point. The singular points of Vdisplaystyle V are those where the ‘test to be a manifold’ fails. See Zariski tangent space.

Once the tangent spaces of a manifold have been introduced, one can define vector fields, which are abstractions of the velocity field of particles moving in space. A vector field attaches to every point of the manifold a vector from the tangent space at that point, in a smooth manner. Such a vector field serves to define a generalized ordinary differential equation on a manifold: A solution to such a differential equation is a differentiable curve on the manifold whose derivative at any point is equal to the tangent vector attached to that point by the vector field.

All the tangent spaces of a manifold may be ‘glued together’ to form a new differentiable manifold with twice the dimension of the original manifold, called the tangent bundle of the manifold.

Formal definitions

The informal description above relies on a manifold's ability to be embedded into an ambient vector space Rmdisplaystyle mathbf R ^m so that the tangent vectors can ‘stick out’ of the manifold into the ambient space. However, it is more convenient to define the notion of a tangent space based solely on the manifold itself.^[2]

There are various equivalent ways of defining the tangent spaces of a manifold. While the definition via the velocity of curves is intuitively the simplest, it is also the most cumbersome to work with. More elegant and abstract approaches are described below.

Definition as the velocity of curves

In the embedded-manifold picture, a tangent vector at a point xdisplaystyle x is thought of as the velocity of a curve passing through the point xdisplaystyle x. We can therefore define a tangent vector as an equivalence class of curves passing through xdisplaystyle x while being tangent to each other at xdisplaystyle x.

Suppose that Mdisplaystyle M is a Ckdisplaystyle C^k manifold (k≥1displaystyle kgeq 1) and that x∈Mdisplaystyle xin M. Pick a coordinate chart φ:U→Rndisplaystyle varphi :Uto mathbf R ^n, where Udisplaystyle U is an open subset of Mdisplaystyle M containing xdisplaystyle x. Suppose further that two curves γ1,γ2:(−1,1)→Mdisplaystyle gamma _1,gamma _2:(-1,1)to M with γ1(0)=x=γ2(0)displaystyle gamma _1(0)=x=gamma _2(0) are given such that both φ∘γ1,φ∘γ2:(−1,1)→Rndisplaystyle varphi circ gamma _1,varphi circ gamma _2:(-1,1)to mathbf R ^n are differentiable in the ordinary sense (we call these differentiable curves initialized at xdisplaystyle x). Then γ1displaystyle gamma _1 and γ2displaystyle gamma _2 are said to be equivalent at 0displaystyle 0 if and only if the derivatives of φ∘γ1displaystyle varphi circ gamma _1 and φ∘γ2displaystyle varphi circ gamma _2 at 0displaystyle 0 coincide. This defines an equivalence relation on the set of all differentiable curves initialized at xdisplaystyle x, and equivalence classes of such curves are known as tangent vectors of Mdisplaystyle M at xdisplaystyle x. The equivalence class of any such curve γdisplaystyle gamma is denoted by γ′(0)displaystyle gamma '(0). The tangent space of Mdisplaystyle M at xdisplaystyle x, denoted by TxMdisplaystyle T_xM, is then defined as the set of all tangent vectors at xdisplaystyle x; it does not depend on the choice of coordinate chart φ:U→Rndisplaystyle varphi :Uto mathbf R ^n.

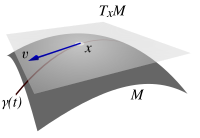
The tangent space TxMdisplaystyle T_xM and a tangent vector v∈TxMdisplaystyle vin T_xM, along a curve traveling through x∈Mdisplaystyle xin M.

To define vector-space operations on TxMdisplaystyle T_xM, we use a chart φ:U→Rndisplaystyle varphi :Uto mathbf R ^n and define a map dφx:TxM→Rndisplaystyle mathrm d varphi _x:T_xMto mathbf R ^n by dφx(γ′(0)) =df ddt[(φ∘γ)(t)]|t=0_t=0. This map turns out to be bijective and may be used to transfer the vector-space operations on Rndisplaystyle mathbf R ^n over to TxMdisplaystyle T_xM, thus turning the latter set into an ndisplaystyle n-dimensional real vector space. Again, one needs to check that this construction does not depend on the particular chart φ:U→Rndisplaystyle varphi :Uto mathbf R ^n being used, and in fact it does not.

Definition via derivations

Suppose now that Mdisplaystyle M is a C∞displaystyle C^infty manifold. A real-valued function f:M→Rdisplaystyle f:Mto mathbf R is said to belong to C∞(M)displaystyle C^infty (M) if and only if for every coordinate chart φ:U→Rndisplaystyle varphi :Uto mathbf R ^n, the map f∘φ−1:φ[U]⊆Rn→Rdisplaystyle fcirc varphi ^-1:varphi [U]subseteq mathbf R ^nto mathbf R is infinitely differentiable. Note that C∞(M)displaystyle C^infty (M) is a real associative algebra with respect to the pointwise product and sum of functions and scalar multiplication.

Pick a point x∈Mdisplaystyle xin M. A derivation at xdisplaystyle x is defined as a linear map D:C∞(M)→Rdisplaystyle D:C^infty (M)to mathbf R that satisfies the Leibniz identity

∀f,g∈C∞(M):D(fg)=D(f)⋅g(x)+f(x)⋅D(g),displaystyle forall f,gin C^infty (M):qquad D(fg)=D(f)cdot g(x)+f(x)cdot D(g),

which is modeled on the product rule of calculus.

If we define addition and scalar multiplication on the set of derivations at xdisplaystyle x by

• 
  (D1+D2)(f) =df D1(f)+D2(f)displaystyle (D_1+D_2)(f)~stackrel textdf=~D_1(f)+D_2(f) and


• 
  (λ⋅D)(f) =df λ⋅D(f)displaystyle (lambda cdot D)(f)~stackrel textdf=~lambda cdot D(f),

then we obtain a real vector space, which we define as the tangent space TxMdisplaystyle T_xM of Mdisplaystyle M at xdisplaystyle x.

The relation between derivations at a point xdisplaystyle x and tangent vectors at xdisplaystyle x is as follows: If γ:(−1,1)→Mdisplaystyle gamma :(-1,1)to M is a differentiable curve initialized at xdisplaystyle x, then the corresponding derivation Dγdisplaystyle D_gamma at xdisplaystyle x is defined by Dγ(f) =df (f∘γ)′(0)displaystyle D_gamma (f)~stackrel textdf=~(fcirc gamma )'(0) (where the derivative is taken in the ordinary sense because f∘γdisplaystyle fcirc gamma is a function from (−1,1)displaystyle (-1,1) to Rdisplaystyle mathbf R ).

Generalizations of this definition are possible, for instance, to complex manifolds and algebraic varieties. However, instead of examining derivations Ddisplaystyle D from the full algebra of functions, one must instead work at the level of germs of functions. The reason for this is that the structure sheaf may not be fine for such structures. For example, let Xdisplaystyle X be an algebraic variety with structure sheaf OXdisplaystyle mathcal O_X. Then the Zariski tangent space at a point p∈Xdisplaystyle pin X is the collection of all kdisplaystyle mathbb k -derivations D:OX,p→kdisplaystyle D:mathcal O_X,pto mathbb k , where kdisplaystyle mathbb k is the ground field and OX,pdisplaystyle mathcal O_X,p is the stalk of OXdisplaystyle mathcal O_X at pdisplaystyle p.

Definition via cotangent spaces

Again, we start with a C∞displaystyle C^infty manifold Mdisplaystyle M and a point x∈Mdisplaystyle xin M. Consider the ideal Idisplaystyle I of C∞(M)displaystyle C^infty (M) that consists of all smooth functions fdisplaystyle f vanishing at xdisplaystyle x, i.e., f(x)=0displaystyle f(x)=0. Then Idisplaystyle I and I2displaystyle I^2 are real vector spaces, and TxMdisplaystyle T_xM may be defined as the dual space of the quotient space I/I2displaystyle I/I^2. This latter quotient space is also known as the cotangent space of Mdisplaystyle M at xdisplaystyle x.

While this definition is the most abstract, it is also the one that is most easily transferable to other settings, for instance, to the varieties considered in algebraic geometry.

If Ddisplaystyle D is a derivation at xdisplaystyle x, then D(f)=0displaystyle D(f)=0 for every f∈I2displaystyle fin I^2, which means that Ddisplaystyle D gives rise to a linear map I/I2→Rdisplaystyle I/I^2to mathbf R . Conversely, if r:I/I2→Rdisplaystyle r:I/I^2to mathbf R is a linear map, then D(f) =def r((f−f(x))+I2)displaystyle D(f)~stackrel textdef=~rleft((f-f(x))+I^2right) defines a derivation at xdisplaystyle x. This yields an equivalence between tangent spaces defined via derivations and tangent spaces defined via cotangent spaces.

Properties

If Mdisplaystyle M is an open subset of Rndisplaystyle mathbf R ^n, then Mdisplaystyle M is a C∞displaystyle C^infty manifold in a natural manner (take coordinate charts to be identity maps on open subsets of Rndisplaystyle mathbf R ^n), and the tangent spaces are all naturally identified with Rndisplaystyle mathbf R ^n.

Tangent vectors as directional derivatives

Another way to think about tangent vectors is as directional derivatives. Given a vector vdisplaystyle v in Rndisplaystyle mathbf R ^n, one defines the corresponding directional derivative at a point x∈Rndisplaystyle xin mathbf R ^n by

∀f∈C∞(Rn):(Dvf)(x) =df ddt[f(x+tv)]|t=0=∑i=1nvi∂f∂xi(x).displaystyle forall fin C^infty (mathbb R ^n):qquad (D_vf)(x)~stackrel textdf=~left.frac mathrm d mathrm d t[f(x+tv)]right

This map is naturally a derivation at xdisplaystyle x. Furthermore, every derivation at a point in Rndisplaystyle mathbf R ^n is of this form. Hence, there is a one-to-one correspondence between vectors (thought of as tangent vectors at a point) and derivations at a point.

As tangent vectors to a general manifold at a point can be defined as derivations at that point, it is natural to think of them as directional derivatives. Specifically, if vdisplaystyle v is a tangent vector to Mdisplaystyle M at a point xdisplaystyle x (thought of as a derivation), then define the directional derivative Dvdisplaystyle D_v in the direction vdisplaystyle v by

∀f∈C∞(M):Dv(f) =df v(f).displaystyle forall fin C^infty (M):qquad D_v(f)~stackrel textdf=~v(f).

If we think of vdisplaystyle v as the initial velocity of a differentiable curve γdisplaystyle gamma initialized at xdisplaystyle x, i.e., v=γ′(0)displaystyle v=gamma '(0), then instead, define Dvdisplaystyle D_v by

∀f∈C∞(M):Dv(f) =df (f∘γ)′(0).displaystyle forall fin C^infty (M):qquad D_v(f)~stackrel textdf=~(fcirc gamma )'(0).

Basis of the tangent space at a point

For a C∞displaystyle C^infty manifold Mdisplaystyle M, if a chart φ=(x1,…,xn):U→Rndisplaystyle varphi =(x^1,ldots ,x^n):Uto mathbf R ^n is given with p∈Udisplaystyle pin U, then one can define an ordered basis ((∂∂xi)p)i=1ndisplaystyle left(left(frac partial partial x^iright)_pright)_i=1^n of TpMdisplaystyle T_pM by

∀i∈1,…,n, ∀f∈C∞(M):(∂∂xi)p(f) =df (∂i(f∘φ−1))(φ(p)).displaystyle forall iin 1,ldots ,n,~forall fin C^infty (M):qquad left(frac partial partial x^iright)_p(f)~stackrel textdf=~(partial _i(fcirc varphi ^-1))(varphi (p)).

Then for every tangent vector v∈TpMdisplaystyle vin T_pM, one has

v=∑i=1nv(xi)⋅(∂∂xi)p.displaystyle v=sum _i=1^nv(x^i)cdot left(frac partial partial x^iright)_p.

This formula therefore expresses vdisplaystyle v as a linear combination of the basis tangent vectors (∂∂xi)p∈TpMdisplaystyle left(frac partial partial x^iright)_pin T_pM defined by the coordinate chart φ:U→Rndisplaystyle varphi :Uto mathbf R ^n.^[3]

The derivative of a map

Every smooth (or differentiable) map φ:M→Ndisplaystyle varphi :Mto N between smooth (or differentiable) manifolds induces natural linear maps between their corresponding tangent spaces:

dφx:TxM→Tφ(x)N.displaystyle mathrm d varphi _x:T_xMto T_varphi (x)N.

If the tangent space is defined via differentiable curves, then this map is defined by

dφx(γ′(0)) =df (φ∘γ)′(0).displaystyle mathrm d varphi _x(gamma '(0))~stackrel textdf=~(varphi circ gamma )'(0).

If, instead, the tangent space is defined via derivations, then this map is defined by

[dφx(X)](f) =df X(f∘φ).displaystyle [mathrm d varphi _x(X)](f)~stackrel textdf=~X(fcirc varphi ).

The linear map dφxdisplaystyle mathrm d varphi _x is called variously the derivative, total derivative, differential, or pushforward of φdisplaystyle varphi at xdisplaystyle x. It is frequently expressed using a variety of other notations:

Dφx,(φ∗)x,φ′(x).displaystyle Dvarphi _x,qquad (varphi _*)_x,qquad varphi '(x).

In a sense, the derivative is the best linear approximation to φdisplaystyle varphi near xdisplaystyle x. Note that when N=Rdisplaystyle N=mathbf R , then the map dφx:TxM→Rdisplaystyle mathrm d varphi _x:T_xMto mathbf R coincides with the usual notion of the differential of the function φdisplaystyle varphi . In local coordinates the derivative of φdisplaystyle varphi is given by the Jacobian.

An important result regarding the derivative map is the following:

Theorem. If φ:M→Ndisplaystyle varphi :Mto N is a local diffeomorphism at xdisplaystyle x in Mdisplaystyle M, then dφx:TxM→Tφ(x)Ndisplaystyle mathrm d varphi _x:T_xMto T_varphi (x)N is a linear isomorphism. Conversely, if dφxdisplaystyle mathrm d varphi _x is an isomorphism, then there is an open neighborhood Udisplaystyle U of xdisplaystyle x such that φdisplaystyle varphi maps Udisplaystyle U diffeomorphically onto its image.

This is a generalization of the inverse function theorem to maps between manifolds.

See also

• Exponential map


• Vector space


• Differential geometry of curves


• Coordinate-induced basis


• Cotangent space

References

• 
  Lee, Jeffrey M. (2009), Manifolds and Differential Geometry, Graduate Studies in Mathematics, Vol. 107, Providence: American Mathematical Society.


• 
  Michor, Peter W. (2008), Topics in Differential Geometry, Graduate Studies in Mathematics, Vol. 93, Providence: American Mathematical Society.


• 
  Spivak, Michael (1965), Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus, W. A. Benjamin, Inc., ISBN 978-0-8053-9021-6.

External links

• 
  Tangent Planes at MathWorld