Odtnhj

In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics. The name "Ext" comes from group theory, as the Ext functor is used in group cohomology to classify abelian group extensions.^[1]

Definition and computation

Let R be a ring and let Mod_R be the category of modules over R. Let B be in Mod_R and set T(B) = Hom_R(A,B), for fixed A in Mod_R. This is a left exact functor and thus has right derived functors RⁿT. The Ext functor is defined by

ExtRn⁡(A,B)=(RnT)(B).displaystyle operatorname Ext _R^n(A,B)=(R^nT)(B).

This can be calculated by taking any injective resolution

0→B→I0→I1→⋯,displaystyle 0to Bto I^0to I^1to cdots ,

and computing

0→HomR⁡(A,I0)→HomR⁡(A,I1)→⋯.displaystyle 0to operatorname Hom _R(A,I^0)to operatorname Hom _R(A,I^1)to cdots .

Then (RⁿT)(B) is the homology of this complex. Note that Hom_R(A,B) is excluded from the complex.

An alternative definition is given using the functor G(A)=Hom_R(A,B). For a fixed module B, this is a contravariant left exact functor, and thus we also have right derived functors RⁿG, and can define

ExtRn⁡(A,B)=(RnG)(A).displaystyle operatorname Ext _R^n(A,B)=(R^nG)(A).

This can be calculated by choosing any projective resolution

⋯→P1→P0→A→0,displaystyle dots to P^1to P^0to Ato 0,

and proceeding dually by computing

0→HomR⁡(P0,B)→HomR⁡(P1,B)→⋯.displaystyle 0to operatorname Hom _R(P^0,B)to operatorname Hom _R(P^1,B)to cdots .

Then (RⁿG)(A) is the homology of this complex. Again note that Hom_R(A,B) is excluded.

These two constructions turn out to yield isomorphic results, and so both may be used to calculate the Ext functor.

Properties of Ext

The Ext functor exhibits some convenient properties, useful in computations.^[2]

• Extⁱ
  _R(A, B) = 0 for i > 0 if either B is injective or A projective.


• The converses also hold:
  
  • If Ext¹
    _R(A, B) = 0 for all A, then Extⁱ
    _R(A, B) = 0 for all A, and B is injective.
  
  
  • If Ext¹
    _R(A, B) = 0 for all B, then Extⁱ
    _R(A, B) = 0 for all B, and A is projective.
  
  


• ExtRn⁡(⨁αAα,B)≅∏αExtRn⁡(Aα,B).displaystyle operatorname Ext _R^nleft(bigoplus nolimits _alpha A_alpha ,Bright)cong prod nolimits _alpha operatorname Ext _R^n(A_alpha ,B).


• ExtRn⁡(A,∏βBβ)≅∏βExtRn⁡(A,Bβ).displaystyle operatorname Ext _R^nleft(A,prod nolimits _beta B_beta right)cong prod nolimits _beta operatorname Ext _R^n(A,B_beta ).


• 
  ExtZn⁡(A,B)=0displaystyle operatorname Ext _mathbb Z ^n(A,B)=0 for all n ≥ 2 abelian groups A and B.


• 
  ExtZ1⁡(Z/p,B)=B/pBdisplaystyle operatorname Ext _mathbb Z ^1(mathbb Z /p,B)=B/pB for all abelian B.^[3]


• Let A be a finitely generated module over a commutative noetherian ring R. Then for every multiplicative set S, all modules B, and all n,

S−1ExtRn⁡(A,B)≅ExtS−1Rn⁡(S−1A,S−1B).displaystyle S^-1operatorname Ext _R^n(A,B)cong operatorname Ext _S^-1R^nleft(S^-1A,S^-1Bright).

• If R is commutative noetherian and A is a finitely generated R-module, then the following are equivalent for all modules B and all n:
  
  • ExtRn⁡(A,B)=0.displaystyle operatorname Ext _R^n(A,B)=0.
  
  
  • For every prime ideal pdisplaystyle mathfrak p of R, ExtRpn⁡(Ap,Bp)=0displaystyle operatorname Ext _R_mathfrak p^n(A_mathfrak p,B_mathfrak p)=0.
  
  
  • For every maximal ideal mdisplaystyle mathfrak m of R, ExtRmn⁡(Am,Bm)=0displaystyle operatorname Ext _R_mathfrak m^n(A_mathfrak m,B_mathfrak m)=0.
  
  

Ext and extensions

Equivalence of extensions

Ext functors derive their name from the relationship to extensions of modules. Given R-modules A and B, an extension of A by B is a short exact sequence of R-modules

0→B→E→A→0.displaystyle 0to Bto Eto Ato 0.

Two extensions

0→B→E→A→0displaystyle 0to Bto Eto Ato 0

0→B→E′→A→0displaystyle 0to Bto E'to Ato 0

are said to be equivalent (as extensions of A by B) if there is a commutative diagram

.

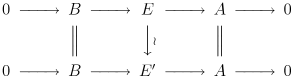Note that the Five Lemma implies that the middle arrow is an isomorphism. An extension of A by B is called split if it is equivalent to the trivial extension

0→B→A⊕B→A→0.displaystyle 0to Bto Aoplus Bto Ato 0.

There is a bijective correspondence between equivalence classes of extensions

0→B→E→A→0displaystyle 0to Bto Eto Ato 0

of A by B and elements of ExtR1⁡(A,B).displaystyle operatorname Ext _R^1(A,B).

The Baer sum of extensions

Given two extensions

0→B→E→A→0displaystyle 0to Bto Eto Ato 0

0→B→E′→A→0displaystyle 0to Bto E'to Ato 0

we can construct the Baer sum, by forming the pullback over Adisplaystyle A,

Γ=g(e)=g′(e′).displaystyle Gamma =left;g(e)=g'(e')right.

We form the quotient

Y=Γ/b∈Bdisplaystyle Y=Gamma /;bin B,

that is, we mod out by the relation (f(b)+e,e′)∼(e,f′(b)+e′)displaystyle (f(b)+e,e')sim (e,f'(b)+e'). The extension

0→B→Y→A→0displaystyle 0to Bto Yto Ato 0

where the first arrow is b↦[(f(b),0)]=[(0,f′(b))]displaystyle bmapsto [(f(b),0)]=[(0,f'(b))] and the second (e,e′)↦g(e)=g′(e′)displaystyle (e,e')mapsto g(e)=g'(e') thus formed is called the Baer sum of the extensions E and E′.

Up to equivalence of extensions, the Baer sum is commutative and has the trivial extension as identity element. The extension 0 → B → E → A → 0 has for its inverse the same extension with exactly one of the central arrows replaced with its negative e.g. the morphism g is replaced by -g.

The set of extensions up to equivalence is an abelian group that is a realization of the functor Ext¹
_R(A, B)

Construction of Ext in abelian categories

The above identification enables us to define Ext¹
_Ab(A, B) even for abelian categories Ab without reference to projectives and injectives (even if the category has no projectives or injectives). We simply take Ext¹
_Ab(A, B) to be the set of equivalence classes of extensions of A by B, forming an abelian group under the Baer sum. Similarly, we can define higher Ext groups Extⁿ
_Ab(A, B) as equivalence classes of n-extensions, which are exact sequences

0→B→Xn→⋯→X1→A→0displaystyle 0to Bto X_nto cdots to X_1to Ato 0

under the equivalence relation generated by the relation that identifies two extensions

ξ:0→B→Xn→⋯→X1→A→0ξ′:0→B→Xn′→⋯→X1′→A→0displaystyle beginalignedxi :0&to Bto X_nto cdots to X_1to Ato 0\xi ':0&to Bto X'_nto cdots to X'_1to Ato 0endaligned

if there are maps X_m → X′_m for all m in 1, 2, ..., n so that every resulting square commutes, i.e. if there is a chain map X:ξ→ξ′displaystyle X:xi to xi '.

The Baer sum of the two n-extensions above is formed by letting X1″displaystyle X''_1 be the pullback of X1displaystyle X_1 and X1′displaystyle X'_1 over A, and Xn″displaystyle X''_n be the pushout of Xndisplaystyle X_n and Xn′displaystyle X'_n under B; see Weibel, §3.4 (but remark there are some errata). Then we define the Baer sum of the extensions to be

0→B→Xn″→Xn−1⊕Xn−1′→⋯→X2⊕X2′→X1″→A→0.displaystyle 0to Bto X''_nto X_n-1oplus X'_n-1to cdots to X_2oplus X'_2to X''_1to Ato 0.

Ring structure and module structure on specific Exts

One more very useful way to view the Ext functor is this: when an element of Extⁿ
_R(A, B) = 0 is considered as an equivalence class of maps f:Pn→Bdisplaystyle f:P_nto B for a projective resolution P∗displaystyle P_* of A ; so, then we can pick a long exact sequence Q∗displaystyle Q_* ending with B and lift the map f using the projectivity of the modules P_m to a chain map f∗:P∗→Q∗displaystyle f_*:P_*to Q_* of degree −n. It turns out that homotopy classes of such chain maps correspond precisely to the equivalence classes in the definition of Ext above.

Under sufficiently nice circumstances, such as when the ring R is a group ring over a field k, or an augmented k-algebra, we can impose a ring structure on ExtR∗(k,k).displaystyle textExt_R^*(k,k). The multiplication has quite a few equivalent interpretations, corresponding to different interpretations of the elements of ExtR∗(k,k).displaystyle textExt_R^*(k,k).

One interpretation is in terms of these homotopy classes of chain maps. Then the product of two elements is represented by the composition of the corresponding representatives. We can choose a single resolution of k, and do all the calculations inside HomR(P∗,P∗),displaystyle textHom_R(P_*,P_*), which is a differential graded algebra, with cohomology precisely Ext_R(k, k).

The Ext groups can also be interpreted in terms of exact sequences; this has the advantage that it does not rely on the existence of projective or injective modules. Then we take the viewpoint above that an element of Extⁿ
_R(A, B) is a class, under a certain equivalence relation, of exact sequences of length n + 2 starting with B and ending with A. This can then be spliced with an element in Ext^m
_R(C, A), by replacing

⋯→X1→A→0and0→A→Yn→⋯displaystyle cdots to X_1to Ato 0quad textandquad 0to Ato Y_nto cdots

with:

⋯→X1→Yn→⋯displaystyle cdots to X_1to Y_nto cdots

where the map X1→Yndisplaystyle X_1to Y_n is the composition of X₁ → A and A → Y_n. This product is called the Yoneda splice.

These viewpoints turn out to be equivalent whenever both make sense.

Using similar interpretations, we find that ExtR∗(k,M)displaystyle textExt_R^*(k,M) is a module over ExtR∗(k,k),displaystyle textExt_R^*(k,k), again for sufficiently nice situations.

Interesting examples

If Z[G]displaystyle mathbb Z [G] is the integral group ring for a group G, then ExtZ[G]∗⁡(Z,M)displaystyle operatorname Ext _mathbb Z [G]^*(mathbb Z ,M) is the group cohomology H*(G,M) with coefficients in M.

If A is a k-algebra, then ExtA⊗kAop∗⁡(A,M)displaystyle operatorname Ext _Aotimes _kA^textop^*(A,M) is the Hochschild cohomology HH*(A,M) with coefficients in the A-bimodule M.

If R is chosen to be the universal enveloping algebra for a Lie algebra gdisplaystyle mathfrak g over a commutative ring k, then ExtR∗⁡(k,M)displaystyle operatorname Ext _R^*(k,M) is the Lie algebra cohomology H∗⁡(g,M)displaystyle operatorname H ^*(mathfrak g,M) with coefficients in the module M.

See also

• Tor functor


• The Grothendieck group is a construction centered on extensions


• The universal coefficient theorem for cohomology is one notable use of the Ext functor


• Grothendieck duality


• Yoneda product

References

• 
  Gelfand, Sergei I.; Manin, Yuri Ivanovich (1999), Homological algebra, Berlin: Springer, ISBN 978-3-540-65378-3
  


• 
  Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.
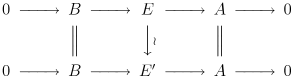